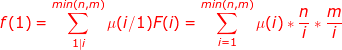P3455 [POI2007]ZAP-Queries
题目描述
Byteasar the Cryptographer works on breaking the code of BSA (Byteotian Security Agency). He has alreadyfound out that whilst deciphering a message he will have to answer multiple queries of the form"for givenintegers aa, bband dd, find the number of integer pairs (x,y)(x,y) satisfying the following conditions:
1le xle a1≤x≤a,1le yle b1≤y≤b,gcd(x,y)=dgcd(x,y)=d, where gcd(x,y)gcd(x,y) is the greatest common divisor of xx and yy".
Byteasar would like to automate his work, so he has asked for your help.
TaskWrite a programme which:
reads from the standard input a list of queries, which the Byteasar has to give answer to, calculates answers to the queries, writes the outcome to the standard output.
FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。
输入输出格式
输入格式:
The first line of the standard input contains one integer nn (1le nle 50 0001≤n≤50 000),denoting the number of queries.
The following nn lines contain three integers each: aa, bb and dd(1le dle a,ble 50 0001≤d≤a,b≤50 000), separated by single spaces.
Each triplet denotes a single query.
输出格式:
Your programme should write nn lines to the standard output. The ii'th line should contain a single integer: theanswer to the ii'th query from the standard input.
输入输出样例
输入样例#1: 复制
2
4 5 2
6 4 3输出样例#1: 复制
3
2
题解:运用莫比乌斯反演
后来发现直接加会TLE,必须优化,对于i~n/(n/i)范围内的值,n/i是相等的,利用该定理可减小时间复杂度
例:n=10
| i | j | i~j | n/(i~j) |
| 1 | 10/(10/1)=1 | 1~1 | 10 |
| 2 | 10/(10/2)=2 | 2~2 | 5 |
| 3 | 10/(10/3)=3 | 3~3 | 3 |
| 4 | 10/(10/4)=5 | 4~5 | 2 |
| 6 | 10/(10/6)=10 | 6~10 | 1 |
#include<iostream>
#include<string.h>
#define ll long long
using namespace std;
ll mu[50007],prime[50007],sum[50007];
bool mark[50007];
void getmu()
{
mu[1]=1;
ll cnt=0;
for(ll i=2;i<50007;i++){
if(!mark[i]){
prime[cnt++]=(ll)i;
mu[i]=-1;
}
for(ll j=0;j<cnt&&i*prime[j]<50007;j++){
mark[i*prime[j]]=1;
if(i%prime[j]){
mu[i*prime[j]]=-mu[i];
}else{
mu[i*prime[j]]=0;
break;
}
}
}
for(int i=1;i<50007;i++)
sum[i]=sum[i-1]+mu[i];
}
int main()
{
int T;
ll b,d,k,ans;
getmu();
scanf("%d",&T);
for(int ca=1;ca<=T;ca++){
scanf("%lld%lld%lld",&b,&d,&k);
if(!k){printf("0
");continue;}
b/=k,d/=k;
if(b>d) swap(b,d);
ans=0;
for(int x=1,y;x<=b;x=y+1){
y=min(b/(b/x),d/(d/x));
ans+=(sum[y]-sum[x-1])*(b/x)*(d/x);
}
printf("%lld
",ans);
}
return 0;
}