题意简述:
求 1 号点到其他点的最短路和其他点到 1 号点的最短路。
思路:
第一眼想到 floyd 但是一看 (1le P,Q le 1e6) 直接暴毙。
再仔细观察题目,发现只需要求1到其他点的最短路和其他点到1的最短路。
你品,你细品。
举个栗子:样例第二组数据:
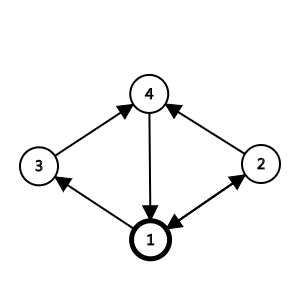
如果我们把这个图反过来建//add(y,x,z)
就成了这个模样:
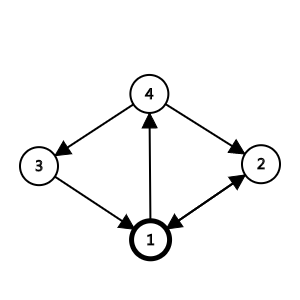
我们惊奇的发现,倒过来建图之后,1 到其他点的最短路就是原来图的其他点到 1 的最短路!
Nice!让我们开始写代码。
代码
几点说明:
- 最短路为标准 Dijkstra ,
spfa已死,Dijkstra当道!(其实这个题应该不卡 spfa )。 - 我采用链式前向星的方式建图,因为要建反图,前缀为 0 的是原图,为 1 的是反图。
#include<bits/stdc++.h>
#define F first
#define S second
using namespace std;
int n,m,nxt[2][1000006],cost[2][1000006],to[2][1000006],h[2][1000006],cnt1,cnt2;
void add(int x,int y,int z) {
to[0][++cnt1]=y;
to[1][++cnt2]=x;
nxt[0][cnt1]=h[0][x];
nxt[1][cnt2]=h[1][y];
cost[0][cnt1]=z;
cost[1][cnt2]=z;
h[0][x]=cnt1;
h[1][y]=cnt2;
}
priority_queue< pair<int,int> >q;
int dis[1000006];
bool vis[1000006];
int dijk(int opt) {
memset(vis,0,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
while(q.size()) q.pop();
dis[1]=0;
q.push(make_pair(0,1));
while(q.size()) {
int u=q.top().S;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=h[opt][u];i;i=nxt[opt][i]) {
int v=to[opt][i];
if(dis[v]>dis[u]+cost[opt][i]) {
dis[v]=dis[u]+cost[opt][i];
q.push(make_pair(-dis[v],v));
}
}
}
int sum=0;
for(int i=1;i<=n;i++)
sum+=dis[i];
return sum;
}
int main() {
int t;
cin>>t;
while(t--) {
memset(nxt,0,sizeof(nxt));
memset(to,0,sizeof(to));
memset(h,0,sizeof(h));
memset(cost,0,sizeof(cost));
cnt1=cnt2=0;
cin>>n>>m;
for(int i=1;i<=m;i++) {
int x,y,z;
cin>>x>>y>>z;
add(x,y,z);
}
int ans1=dijk(0),ans2=dijk(1);
cout<<ans1+ans2<<endl;
}
return 0;
}
其他
双倍经验放送:SP50