小白初识 归并排序（MergeSort）

归并排序是一种典型的用分治的思想解决问题的排序方式。

它的原理就是：将一个数组从中间分成两半，对分开的两半再分成两半，直到最终分到最小的单位（即单个元素）的时候，

将已经分开的数据两两合并，并且在合并的同时进行排序（先分解，再合并）。

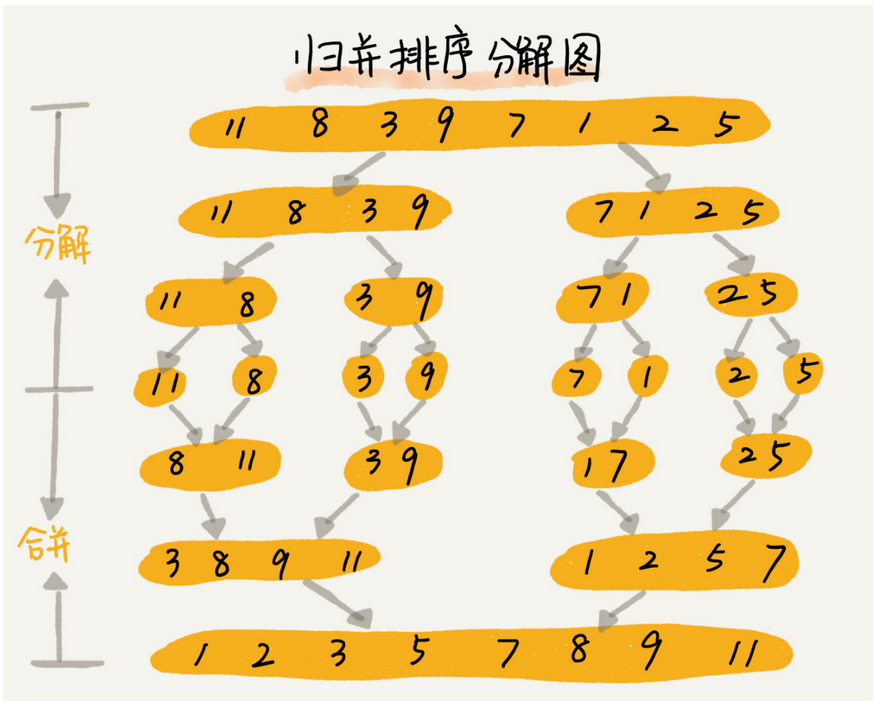
将一个大的问题分而治之，拆分成若干个小问题，这就是分治的思想。

拆分不成问题，但是合并的时候稍微麻烦一些。合并的时候需要对合并的数据挨个儿排序。

我用Java实现了归并排序：

package com.structure.sort;

/**
 * @author zhangxingrui
 * @create 2019-01-24 21:22
 **/
public class MergeSort {

    public static void main(String[] args) {
        int[] numbers = {9, 1, 2, 8, 7, 3, 6, 4, 3, 5, 0, 9, 19, 39, 25, 34, 17, 24, 23, 34, 20};
        // 归并排序借助递归来实现，重要的是要找到递归的终结条件（不然容易发生堆栈异常）
        // 递推公式：mergeSort(p...r) = merge(p, q) + merge(q+1, r)
        // 终结条件：p >= r
        mergeSort(numbers, 0, numbers.length - 1);
        for (int number : numbers) {
            System.out.println(number);
        }
    }

    /**
     * @Author: xingrui
     * @Description: 归并排序
     * @Date: 21:26 2019/1/24
     */
    private static void mergeSort(int[] numbers, int p, int r){
        if(p >= r)
            return;
        int q = (p + r) / 2;
        mergeSort(numbers, p, q);
        mergeSort(numbers, q + 1, r);
        merge(numbers, p, q, r);
    }

    /**
     * @Author: xingrui
     * @Description: 合并数组
     * @Date: 21:35 2019/1/24
     */
    private static void merge(int[] numbers, int p, int q, int r){
        int[] temp = new int[r - p + 1];
        int i = p;
        int j = q + 1;
        int k = 0;

        while (i <= q && j <= r){
            if(numbers[i] <= numbers[j]){
                temp[k++] = numbers[i++];
            }else{
                temp[k++] = numbers[j++];
            }
        }

        while (i <= q)
            temp[k++] = numbers[i++];

        while (j <= r)
            temp[k++] = numbers[j++];


        for (int number : temp) {
            numbers[p++] = number;
        }
    }

}

像上面的代码看到的，拆分的时候都是从中间拆分：

private static void mergeSort(int[] numbers, int p, int r){
        if(p >= r)
            return;
        int q = (p + r) / 2;
        mergeSort(numbers, p, q);
        mergeSort(numbers, q + 1, r);
        merge(numbers, p, q, r);
    }

所以这里每次都要(p + r) / 2 得到我们想要的中间位置。

代码实现起来很容易，那么我们再来分析一下归并排序：

1.归并排序是稳定的排序算法吗（即数组中有相同的元素，在排序结束时候，相同的元素的前后关系并没有发生变化）？

2.归并排序是原地排序吗（空间复杂度为O(1)就可以叫做原地排序）？

3.归并排序的时间复杂度怎么计算？

解答：

1.归并排序是稳定的排序的算法。我们可以看看发生元素位置交换的地方：

while (i <= q && j <= r){
            if(numbers[i] <= numbers[j]){
                temp[k++] = numbers[i++];
            }else{
                temp[k++] = numbers[j++];
            }
        }

i比j小，所以numbers[i]永远在numbers[j]的前面，当numbers[i] = numbers[j]的时候，我们是把numbers[i]放到了temp里面，

所以归并排序下来，相同的元素的前后关系没有发生变化。

 

2.归并排序不是原地排序。这个很明显，在merge过程中需要申请一个temp数组来临时存储数据，而这个temp数组大小不确定。

3.归并排序的时间复杂度是O(nlogn)。这个就需要推导一下了：

首先我们得知道归并排序怎么用表达式表达出来：

T(p...r) = T(p...q) + T(q+1...r) + k，其中k是合并两段数组需要的时间。

假设我们对n个元素进行排需要的时间为：T(n)，那么对n/2个数组排序需要的时间就是T(n/2)，合并数组的时间复杂度就是O(n)

我们可以得出以下公式：

T(1) = C （C表示一个常量级别的时间）

T(n) = 2 * T(n/2) + n

以此类推：

T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
= 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
......
= 2^k * T(n/2^k) + k * n
......

得到了2^k * T(n/2^k) + k * n，那么当T(n/2^k) = 1的时候，即n/2^k = 1，k=log2n，

再将k值代入2^k * T(n/2^k) + k * n中可得：T(n) = Cn + nlog2n，根据时间复杂的计算原则，取大的数nlog2n，

所以归并排序的时间复杂的就是O(nlogn)，并且从上面的代码中也可以看到对于归并排序而言，它的执行效率与

要执行排序的数组的有序度无关，即最大最小平均时间复杂度都是O(nlogn)。