hdu3976(Electric resistance) 高斯消元 的题解 :转自 https://www.cnblogs.com/ACRykl/p/8711227.html
Electric resistance
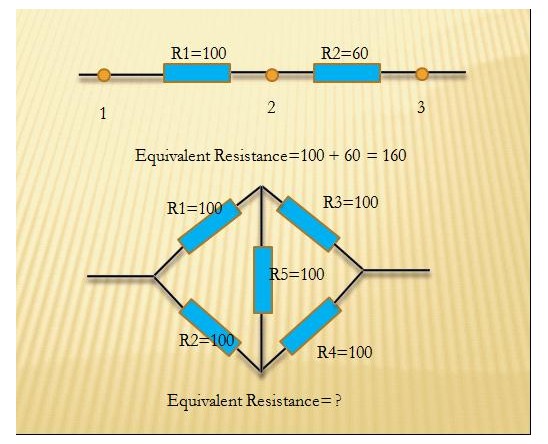
总体思路:利用 节点电压法 列线性方程,然后高斯消元法求解。
① 先普及一下知识:
节点:电路中三条或三条以上支路的交点。
参考点:任选的一个个点,把该点作为电路的的电位参考点,
通常选择为一个节点,因为多出了一个节点没用
节点电压:节点与参考点之间的电压
独立源:包含电压源和电流源。
电流源:电流不受外电路的影响而独立存在的电源。
电导:电阻的倒数。
自导:就是该节点所连的支路电导之和,
如 G(11) 就是 1 号节点所连的各支路电导之和。
互导:相邻节点间公共电导之负值,
如 G(1,2) 就是1 号节点和 2 号节点之间的电导之和的负值。
一般的,对于有 n 个节点的电路应用 KCL 列方程式时,只能写出 n-1 个独立方程,
且为任意 n-1 个,这 n-1 个称为 独立节点,节点分析法可以从 KCL 推导证明(这里就不讲了)
所以我们用 节点分析法时,只需要用到 n-1 个节点
② 以节点电压为待求的电路变量,求解电路。

(注意这里的 n 为 结点数 - 1 )
对于第一个矩阵,主对角线上的元素为:自导
其余元素为:互导
对于第二个矩阵,其值为对应节点的节点电压,如 U1 为 1 号节点的节点电压
对于第三个矩阵,xi 代表: 连接到该节点各支路中独立源所引起的电流代数和
对于电流源产生的电流,当流入节点时为正,反之为负;
对于电压源产生的电流,当电压源正极靠近该节点时为正,反之为负。
③ 将上述矩阵展开 得到 n 个方程 (再提醒一次,这里的 n 是:结点数-1 )
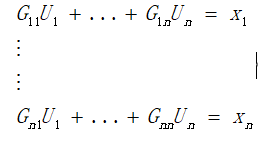
于是有增广矩阵:

③ 具体思路
节点电压法就是通过电流和电阻求解电压,而这道题没给出电压,我们就自己外加电压源,
为了计算方便,我们就在 节点1 和 节点 n 之间外加电流源,为什么是电流源呢?当然是为了 容易求电流了,
而且 既然追求简单,我们自然要贯彻到底,就可以设电流源流出的电流 为 1.,
而且 上面我已经强调过几次了,我们只需要用到 n-1 个节点,所以 我们可以不用 节点1 并设其电压为 0.
这样子 我们就可以列增广矩阵,求解 各节点电压,然后 用
(节点 n 的电压 - 0 (节点 1的电压)) / 1(节点1和节点n 之间的 总电流)= 等效电阻
化简一下就是, 节点 n 的电压 = 等效电阻
为了更直观,我用题目的下标再画一个增广矩阵矩阵吧。
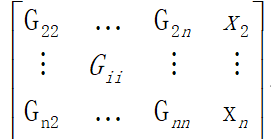
注意节点1 是不用求的,所以我们只用到 节点2 到 节点n. 而我的代码里的增广矩阵是从下标 0 开始的,
各位要看清楚,a[0][0] 对应的是 G21,即 节点1 和 节点 2 之间电阻的倒数。
而且 各节点间只有 节点1 和 节点n 之间有独立电流源引起的电流,所以 x1 和 xn 为 1 (当然,x1 没用到),其他皆为 0
证明:节点电压法可列 必有解 (还不会证明,等我线代学完)
首先,我们先 观察一下 n 个节点,n 个方程的增广矩阵,注意一下,这里多列了一条线性没有贡献的方程,但不止多了一行,而且多了一列。
原先是 (n-1)*(n-1+1) ,现在是 n*(n+1)的矩阵。(+1 是因为有一列常数项向量)的矩阵)
因为这样比较容易看出 节点电压法所列的增广矩阵的特点。

特点①:系数矩阵 是关于主对角线对称的,即 G( i , j )=G( j , i )
特点②:系数矩阵的每一行加起来和为 0,如:G(1,1)= - (G(1,2) + G(1,3) + ..+ G(1,n)),所以 G(1,1)+G(1,2) + G(1,3) + ..+ G(1,n) = 0
Let's go back to 节点方程所列的增广矩阵,怎么证明该方程必有解呢?
我们将线性方程组记为: Ax=B,只要 A 可逆,x 必有解
其中 A 为系数矩阵, B 为 常数项向量,那么怎么证明 A 可逆呢?
只要 A 满足 两个条件,A 为方阵,且 det(A) != 0 即可,
于是,对于 A 对应的行列式:
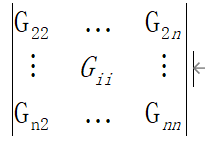
============ ========= ========= ======= ====== ===== ===== === == =
一剪梅·舟过吴江 宋代: 蒋捷
何日归家洗客袍?银字笙调,心字香烧。