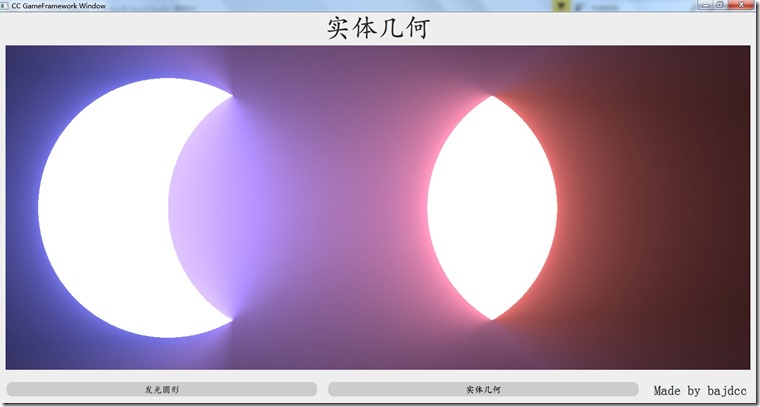
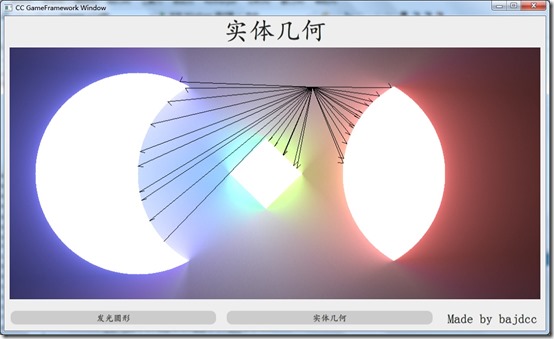
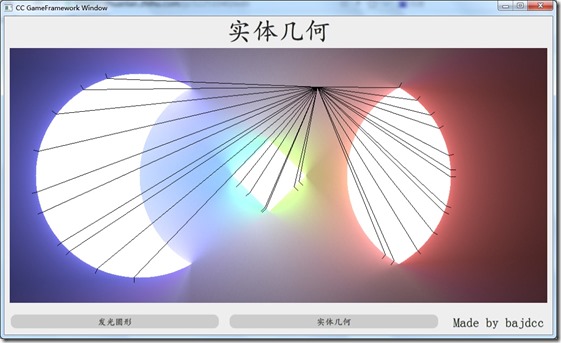
在上篇文章的基础上,做了许多调整,修复了许多BUG。在解决bug的过程中,我逐渐领悟到一个要领:枯燥地一步步调试太痛苦了,找不到问题的根源!所以我选择将中间结果打到图片上。如:
(注意,里面的点是我随便点的,有互动了吧)
这就非常爽了!
本文分两个部分,一个是交并差的实现,一个是矩形的实现。
基本数据结构
// 点信息 struct Geo2DPoint { Geo2DPoint(); Geo2DPoint(float distance, const vector2& position, const vector2& normal); const Geo2DPoint& operator = (const Geo2DPoint& r); float distance{ FLT_MAX }; // 光线起点到交点距离 vector2 position; // 交点位置 vector2 normal; // 交点法向量(指向物体外部) }; // 相交测试 struct Geo2DResult { Geo2DResult(); Geo2DResult(const Geo2DShape* body, bool inside, Geo2DPoint min_pt, Geo2DPoint max_pt); Geo2DResult(const Geo2DResult& r); const Geo2DResult& operator = (const Geo2DResult& r); const Geo2DShape* body{ nullptr }; bool inside{ false }; Geo2DPoint min_pt, max_pt;//交点较小解和较大解的信息 };
每次发出一道光线,需要计算:
- 如果光线与某物体相交,返回该物体指针body
- 光线起点是否在物体内部inside
- 光线与物体最近的交点信息,包括交点坐标、光线起点到交点的距离、交点法线,如果此时光线起点位于物体内部,那么交点可能不是最近的(因为这里的最近指的是解二次方程时的较小根)
- 光线与物体最远的交点信息
说明:
- 即使光线与物体未有交点,还是要计算出所有交点信息
- 不只是最近的交点信息很重要,最远的交点同样重要
原因:
- 上面的数据结构是为了解决图形间交并差的问题!!
- 如两圆相交,ABAB的光线路径,那么光线与物体相交的两个点不同时是光线离A、B的最近点,所以最远点的信息是必须要计算的
- 为什么要用inside?同样是与A、B相交,光线起点在物体内部和在物体外部所产生的效果是不一样的!因为我们还要计算法线呢!
- ……因此促成了现在的数据结构
图形间的交、并、差
上一篇文章中,虽然实现了交并差,但是还不完善:交点信息和法向量没有计算正确,因此做了调整(并集没有调整):
【计算交集】
https://github.com/bajdcc/GameFramework/blob/master/CCGameFramework/base/pe2d/Geometries2D.cpp#L70
if (op == t_intersect) { const auto r1 = obj1->sample(ori, dst); if (r1.body) { const auto r2 = obj2->sample(ori, dst); if (r2.body) { const auto rd = ((r1.inside ? 1 : 0) << 1) | (r2.inside ? 1 : 0); switch (rd) { case 0: // not(A or B) if (r1.min_pt.distance < r2.min_pt.distance) { if (r2.min_pt.distance > r1.max_pt.distance) // AABB break; if (r2.max_pt.distance < r1.max_pt.distance) // ABBA return r2; auto r(r2); // ABAB r.max_pt = r1.max_pt; return r; } if (r2.min_pt.distance < r1.min_pt.distance) { if (r1.min_pt.distance > r2.max_pt.distance) // BBAA break; if (r1.max_pt.distance < r2.max_pt.distance) // BAAB return r1; auto r(r1); // BABA r.max_pt = r2.max_pt; return r; } break; case 1: // B if (r1.min_pt.distance < r2.max_pt.distance) { if (r1.max_pt.distance > r2.max_pt.distance) // ABA { auto r(r1); r.max_pt = r2.max_pt; return r; } else // AAB { auto r(r1); r.max_pt = r1.max_pt; return r; } } break; case 2: // A if (r2.min_pt.distance < r1.max_pt.distance) { if (r2.max_pt.distance > r1.max_pt.distance) // BAB { auto r(r2); r.max_pt = r1.max_pt; return r; } else // BBA { auto r(r2); r.max_pt = r2.max_pt; return r; } } break; case 3: // A and B if (r1.min_pt.distance > r2.min_pt.distance) { if (r1.max_pt.distance > r2.max_pt.distance) // BA { auto r(r2); r.min_pt = r1.min_pt; return r; } else // AB { return r1; } } else { if (r2.max_pt.distance > r1.max_pt.distance) // AB { auto r(r1); r.min_pt = r2.min_pt; return r; } else // AB { return r2; } } default: break; } } } }
【计算差集】
这里注意的是某些情况下需要做法向量翻转
https://github.com/bajdcc/GameFramework/blob/master/CCGameFramework/base/pe2d/Geometries2D.cpp#L171
if (op == t_subtract) { const auto r1 = obj1->sample(ori, dst); const auto r2 = obj2->sample(ori, dst); const auto rd = ((r1.body ? 1 : 0) << 1) | (r2.body ? 1 : 0); switch (rd) { case 0: // not(A or B) break; case 1: // B break; case 2: // A if (r1.inside) // AA { if (r2.max_pt.distance == FLT_MAX) return r1; if (r1.min_pt.distance > r2.max_pt.distance) return r1; auto r(r1); r.min_pt = r2.max_pt; r.min_pt.normal = -r.min_pt.normal; return r; } else return r1; case 3: // A and B if (r1.inside && r2.inside) { if (r2.max_pt.distance < r1.max_pt.distance) // BA { auto r(r1); r.min_pt = r2.max_pt; r.min_pt.normal = -r.min_pt.normal; r.inside = false; return r; } else // AB { break; } } else if (r2.inside) { if (r1.max_pt.distance > r2.max_pt.distance) { if (r2.max_pt.distance > r1.min_pt.distance) // ABA { auto r(r1); r.min_pt = r2.max_pt; r.min_pt.normal = -r.min_pt.normal; r.inside = false; return r; } else // BAA { return r1; } } else // AAB break; } else if (r1.inside) // BAB { auto r(r1); r.max_pt = r2.min_pt; return r; } else { if (r1.min_pt.distance < r2.min_pt.distance) { if (r2.min_pt.distance > r1.max_pt.distance) // AABB return r1; if (r2.max_pt.distance < r1.max_pt.distance) // ABBA return r1; auto r(r1); // ABAB r.max_pt = r2.min_pt; r.max_pt.normal = -r.max_pt.normal; return r; } else { if (r1.min_pt.distance > r2.max_pt.distance) // BBAA return r1; if (r1.max_pt.distance < r2.max_pt.distance) // BAAB break; auto r(r1); // BABA r.min_pt = r2.max_pt; r.min_pt.normal = -r.min_pt.normal; return r; } } default: break; } }
想知道代码为什么这么写,需要拿张纸比划一下(逃
为什么这么多if???因为我可以调试啊(最开始两张图),当什么问题都解决完的时候,代码就变这么长了。
矩形的实现
一开始圆的实现非常简单,因为算个距离很快,法向量就更简单,而矩形不同。
【矩形】
static int SignBit(const float& a)//返回a的符号 { if (fabs(a) < EPSILON) { return 0;//接近0 } return a > 0 ? 1 : -1; } static bool IntersectWithLineAB(const vector2& ori, const vector2& dir, const vector2& p1, const vector2& p2, float& t, vector2& p) { //利用直线的参数方程计算一直线与另一直线的交点 const auto tAB1 = dir.y * (p2.x - p1.x) - dir.x * (p2.y - p1.y);//计算平行 if (fabs(tAB1) > EPSILON)//不平行必有交点 { t = ((ori.x - p1.x) * (p2.y - p1.y) - (ori.y - p1.y) * (p2.x - p1.x)) / tAB1;//计算距离 p = ori + dir * t;//计算交点 return (SignBit(p1.x - p.x) == SignBit(p.x - p2.x)) && (SignBit(p1.y - p.y) == SignBit(p.y - p2.y));//交点是否在p1p2间 } return false;//两直线平行,无交点 } Geo2DResult Geo2DBox::sample(vector2 ori, vector2 dir) const { const auto _A = vector2(costheta * -s.x + sintheta * -s.y, costheta * -s.y - sintheta * -s.x); const auto _B = vector2(costheta * s.x + sintheta * -s.y, costheta * -s.y - sintheta * s.x); const auto A = center + _A; const auto B = center + _B; const auto C = center - _A; const auto D = center - _B; const vector2 pts[4] = { A,B,C,D }; static int m[4][2] = { {0,1},{1,2},{2,3},{3,0} }; float t[2];//保存两交点的距离 vector2 p[2];//保存两交点的位置 int ids[2];//保存与矩形哪一条边相交 int cnt = 0; for (int i = 0; i < 4 && cnt < 2; i++) { if (IntersectWithLineAB(ori, dir, pts[m[i][0]], pts[m[i][1]], t[cnt], p[cnt])) { ids[cnt++] = i; } } if (cnt == 2)//有两个交点 { const auto td = ((t[0] >= 0 ? 1 : 0) << 1) | (t[1] >= 0 ? 1 : 0); switch (td) { case 0: // 双反,无交点,在外 break; case 1: // t[1],有交点,在内 //只与t1相交,那么t0肯定是另一交点,p0肯定为负 return Geo2DResult(this, false, Geo2DPoint(t[0], p[0], Normalize(pts[m[ids[0]][0]] + pts[m[ids[0]][1]] - center - center)), Geo2DPoint(t[1], p[1], Normalize(pts[m[ids[1]][0]] + pts[m[ids[1]][1]] - center - center))); case 2: // t[0],有交点,在内 //只与t0相交,那么t1肯定是另一交点,p1肯定为负 return Geo2DResult(this, false, Geo2DPoint(t[1], p[1], Normalize(pts[m[ids[1]][0]] + pts[m[ids[1]][1]] - center - center)), Geo2DPoint(t[0], p[0], Normalize(pts[m[ids[0]][0]] + pts[m[ids[0]][1]] - center - center))); case 3: // 双正,有交点,在外 if (t[0] > t[1])//都相交?就看看哪个交点更近了 { return Geo2DResult(this, false, Geo2DPoint(t[1], p[1], Normalize(pts[m[ids[1]][0]] + pts[m[ids[1]][1]] - center - center)), Geo2DPoint(t[0], p[0], Normalize(pts[m[ids[0]][0]] + pts[m[ids[0]][1]] - center - center))); } else { return Geo2DResult(this, false, Geo2DPoint(t[0], p[0], Normalize(pts[m[ids[0]][0]] + pts[m[ids[0]][1]] - center - center)), Geo2DPoint(t[1], p[1], Normalize(pts[m[ids[1]][0]] + pts[m[ids[1]][1]] - center - center))); } default: break; } } return Geo2DResult(); }
其实过程不复杂(我一晚上竟然能搞定哈哈,这归功于调试方法的先进性),计算法向量很简单,就是两个对角线的叠加方向。。
有几个注意点:
- 求符号SignBit自己写的,用fsignbit导致gg(算我不会用吧),我相信编译器的优化能力
- 知矩形中心点、两轴距离、旋转角度后,要计算出四点的坐标,这时有计算顺序,一开始只能将旋转矩阵应用于(sx,sy)轴向量!不能用于四点的真实坐标,相当于先在矩形的本地坐标系中应用旋转,最后才加上矩形自身的位置偏移
- 为什么要用参数方程做,不用y=kx+b做:如果这时的直线是竖直方向的呢?y=kx+b就不能表达了
- 求出了交点,要判断交点是否在线段AB上,做法是x坐标和y坐标相减判断同符号,不能用y=kx+b算距离求比值在0~1间,这样即不正确也不高效
小结
矩形会做之后,多边形应该都能搞定了,如三角形,只要考虑一下三边的方向即向(即判断是在内还是在外)。
做完之后,在做反射、折射,这简单了!因为距离呀交点呀法向量全部求出来了。
至于我为什么要在框架中实现这个效果:一者,可视化+互动;二者,与众不同;三者,框架要有例子才能证明好用啊。