前置知识:
简单 ( ext{dp}),队列。
首先我们看一道题目:原题链接
简要题意:
给定一个长为 (n) 的数组,要求 不能选连续超过 (m) 个数,问选出数的最大值。
(n leq 10^5 , a_i leq 10^9).
注:本题将作为 作者讲解单调队列优化 ( ext{dp}) 的引子题。
(mathcal{O}(nm)) 的 ( ext{dp})
首先我们考虑用 (f_i) 来表示 ([1,i]) 的答案,但是你会发现一个问题:你不知道 (i) 选不选,就意味着你不知道 前面能选 (m) 个还是只能选 (m-1) 个(连续),无法进行操作。
于是我们用 (f_{i,0}) 表示 ([1,i]) 中 不选 (i) 的答案。
(f_{i,1}) 表示 ([1,i]) 中 选 (i) 的答案。
这样我们可以列出这样的状态转移方程:
只需要先算出 (f_{i,0}),再算 (f_{i,1}),可以保证无后效性。这样一个可实现的 ( ext{dp}).
可是这时间复杂度是 (mathcal{O}(nm^2)) 的,无法通过。
一个显然的优化,用 (s) 表示 (a) 的前缀和,这样就变成了:
时间复杂度会是 (mathcal{O}(nm)),仍然无法通过。
那么如何优化这个 ( ext{dp}) 呢?
你考虑到 (f_{i,1}) 的决策实际上是连续的一段:([i-m , i-1]) 区间。
所以我们可以用 单调队列优化。
模板题:单调队列优化 ( ext{dp})
单调队列有啥用?
首先,我们知道,队列里可以有很多元素。
下面我们将用集合的形式来表示队列或数组,如 ({ 1,2,4}) 则表示队列中依次有元素 (1,2,4),或者是一个长度为 (3) 的序列,其元素依次为 (1,2,4).
假设我们有一个队列 ({ a_1 , a_2 cdots a_n}),你会发现,如果你要从其中取出一个 最大值,此时你必须遍历队列(你需要用另一个数据结构存储 (a),并将队列一个个弹出,然后再重新维护 (a)),需要 (mathcal{O}(n)).
那么这样一道题目就来了:
(n) 个数,给定 (m),对每个 (1 leq i leq n),求 (max_{j= max(1,i-m+1)}^{i} a_j).
数据范围:(n,m leq 2 imes 10^7),(a) 给出随机生成器(略)。
时间限制:(500ms).
本质就是求连续 (m) 个数的最大值。
诚然你可以用 (f_i) 表示答案,然后 (mathcal{O}(nm)) 求出。
当然你也可以用高级数据结构(线段树等)来维护连续一段的最大值,这样是 (mathcal{O}(n log m)).
但是限于本题 (2 imes 10^7) 的数据,无法通过。
我们需要一个 (mathcal{O}(n)) 的算法。
这时,单调队列的应用就到了。
单调队列是啥?
首先我们要知道单调队列是什么。
对于一个队列 (q) 中的元素 ({ a_1 , a_2 cdots a_n}),如果在操作时能 时时保证 (a) 的有序性,则 (q) 为单调队列。
通常,我们有 priority_queue 来实现,需要单次 (log) 的复杂度。如果用堆也一样。
但是,现在,对于 连续一段数的极值,我们可以用特殊的方式实现。
单调队列的维护(引子)
我们用单调队列来维护 对当前位置有决策性作用的节点。
比方说一个数组 ({3 , 2 , 1}),对 (1) 有决策性作用的节点有 (3,2,1).
但是数组 ({1 , 2 , 3}),对 (3) 有决策性作用的节点就只有 (3).
- 如何理解?
对已经失去决策性作用的节点,出队;否则入队。
- 什么是失去决策性作用?
这样可以做到 (mathcal{O}(n)) 的维护。
- 这些都是啥?
单调队列的维护(正题)
下面我们用一个例子来解释。
对于 ({ 1,4,3,5,2}) 求解上述问题,(m=3),如何快速得解呢?
起初单调队列为空。
然后,对于 (1) 号节点,显然决策只有一个:

所以 (f_1 = 1),这是显然的。
此时 (a_2 = 4) 进来了,我们发现,对于 (i geq 2) 的节点 (a_2 > a_1),所以称 (a_1) 失去了决策性作用。因为只要 (a_1) 会被取到,那么 (a_2) 也会被取到,而 (a_2 > a_1),所以 (a_1) 已经失去了决策性。
那么我们把 ( ext{front} - a_1) 踢出。
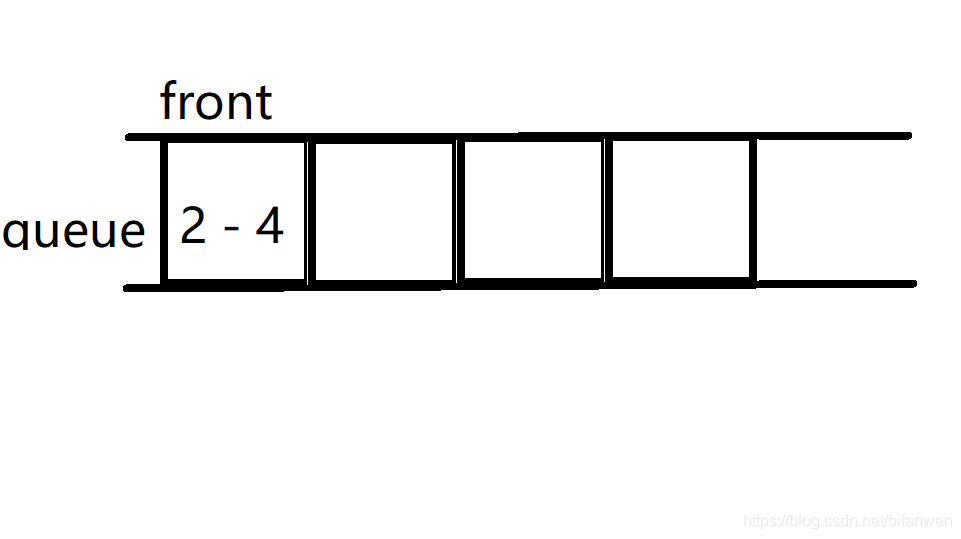
(2-4) 表示 (a_2 = 4).
这时 (f_2 = 4),显然。
下面 (a_3 = 3) 进队之后,(3) 有没有必要弹出呢?如果弹出,(3) 在队尾又如何弹出呢?
不需要。因为,此时尽管 (a_2 > a_3),但对于 (i geq 3),并不是当 (a_3) 能被取到时,(a_2) 就会被取到。因为 (a_5) 的决策会来自 (a_3) 而不是 (a_2),所以不应弹出 (a_3),也不应弹出 (a_2),就把 (a_3 = 3) 插入在队尾。
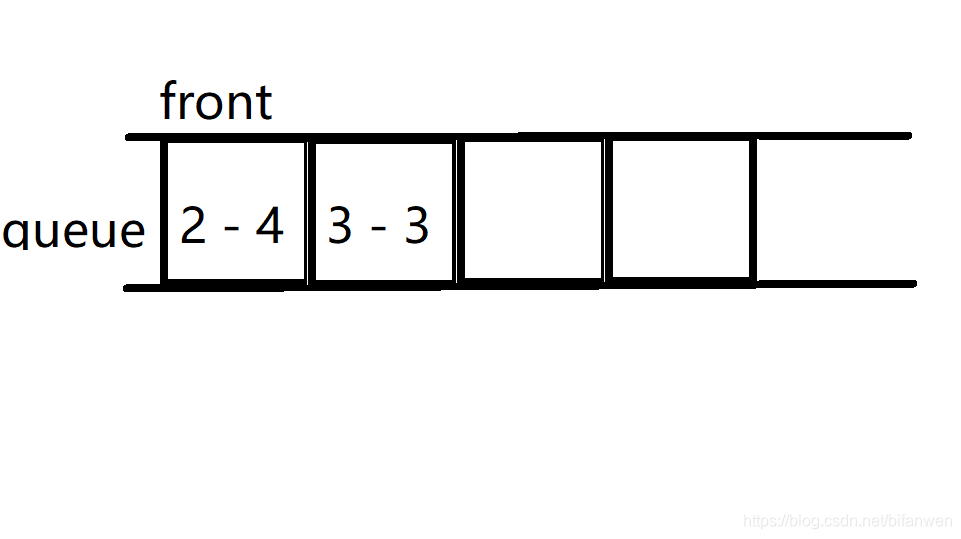
然后你会发现 ( ext{front}) 永远维护最大值。因为如果队头不是最优的,显然 队头比其它任何节点下标小,所以队头还在只能说明它是最优的,否则它就会失去决策性。
这样,(f_3 = 4).
下面 (a_4 = 5),显然 (4) 和 (3) 都可以卷铺盖走人了,因为 (5 > 4 > 3),社会的竞争如此激烈。
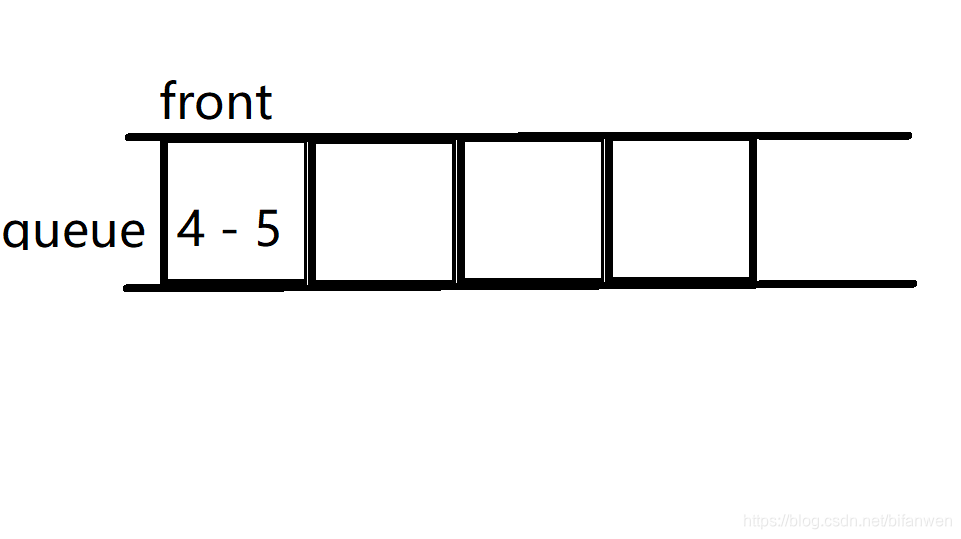
这样的话,(f_4 = 5),没有问题。
然后 (a_5 = 3) 进来之后,一样的道理,同时保留 (5) 和 (3).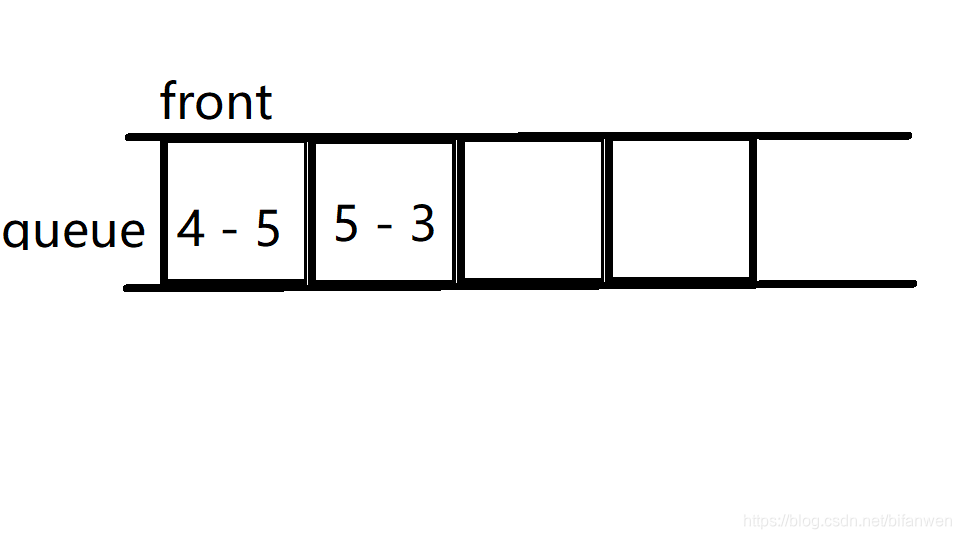
此时 (f_5 = 5).
所以对于数组 ({ 1,4,3,5,2}),对应的 (f) 为 ({ 1,4,4,5,5}),没有问题。
初学者大概都会问:
queue还是priority_queue呢?
诚然是 queue,因为 对决策性的操作 已经保证了单调性,如果用优先队列反而会多一个 (log) !
例题和配套代码
实际上,上面的题目仅仅是 洛谷 ( ext{P1440}) 的一个改版,把最小值改成了最大值而已。
顺便说一句,这个题似乎 (mathcal{O}(n log m)) 的微妙卡常是可以通过的
回归正题
说了这么多,希望你也知道单调队列优化 ( ext{dp}) 大概是个啥了吧。
回归这题的转移方程式:
而 (s_i) 是不变的,实际上可以变形为:
(f{i,1}) 的决策是连续的一段,只需要用单调队列取出 (f_{x,0} -s_x) 最大的节点即可。