3.3分析卷积乘法优化的复用

分析tile并行算法的优化情况：

一维卷积的复用情况分析

比如8个元素的一维卷积tile优化．

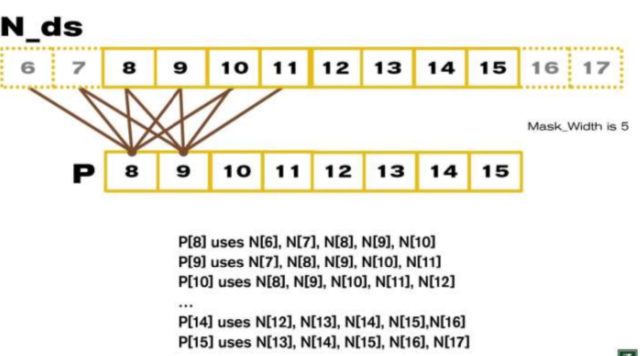
M的大小是５,计算８个元素的卷积需要载入 8+5-1 =12, 如果不使用tile，每个元素都需要载入 8*5 =40,  所以全局内存访问带宽减少 40/12 =3.3．　

正常我们算40 = 8＊５的方式来看，可以换另外一种方式来看，可以得到规律：

可以看出来，N[6] 使用了一次，N[7]使用了２次，N[8]３次，N[９]４次，N[10,11,12,13]都是５次,N[14] 4次．．．

一共是：　1+2+3+4+5*(8-5+1)+4+3+2+1 = 10+20+10 = 40 , 40/12 =3.3

总结规律:

１+2 +.... + MASK_WIDTH-1+ MASK_WIDTH*(O_TILE_WIDTH-MASK_WIDTH+1) +  MASK_WIDTH-1 +....+2+1

= MASK_WIDTH * (MASK_WIDTH-1) + MASK_WIDTH*(O_TILE_WIDTH-MASK_WIDTH+1) 

= MASK_WIDTH*O_TILE_WIDTH

所以减少访问的比例是：

reduction ratio =  (MASK_WIDTH*O_TILE_WIDTH) / (O_TILE_WIDTH+MASK_WIDTH-1) = (5*8)/(8+5-1) = 3.3

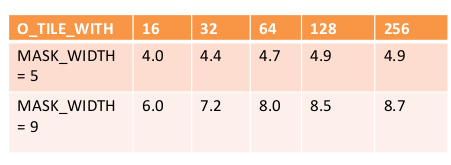可以看出这个比例是随着O_TILE_WIDTH 增加而变大，随着MASK_WIDTH增大而变大．

 /二位卷积的复用情况分析

结合上面的规律可以知道，一共有(O_TILE_WIDTH+MASK_WIDTH-1)² 会载入到sharedMemory中，不使用tile,会由(MASK_WIDTH*O_TILE_WIDTH)²次全局内存访问(global memory)．

减少访问的比例是reduction ratio =   (MASK_WIDTH*O_TILE_WIDTH)²   / (O_TILE_WIDTH+MASK_WIDTH-1)² 

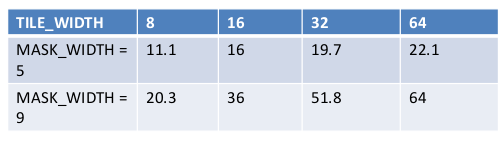可以看出这个比例是随着O_TILE_WIDTH 增加而变大，随着MASK_WIDTH增大而变大．