Trie图(蒟蒻听说AC自动机能做的题Trie图都能做,而且AC自动机可能被卡,就没学过AC自动机),最近想捡一捡,好久之前做的了。
Trie图,就是一个在Trie树上建的图 大概描述一下
比如说有几个字符串:
abc
abcd
bcd
bacd
jdr
ac
先把它们存在Trie树中:
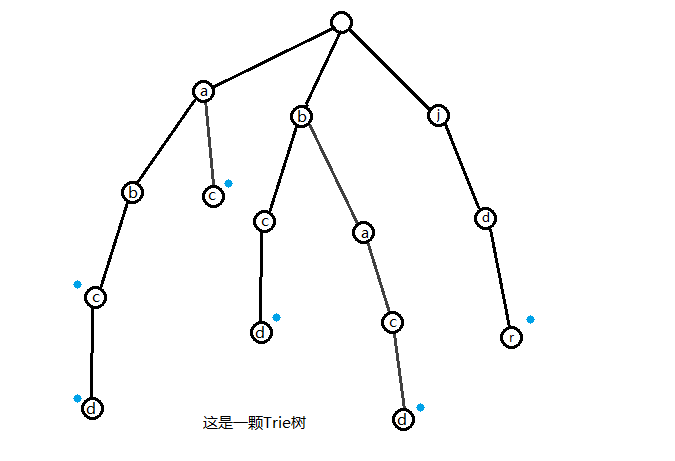
就像KMP那样,做出这样的逻辑判断:
bacd比较到第三位bac结果没有d,但起码bac有了,所以以bac为前缀的或以bac后缀为前缀的串是不用再比较前缀了。
所以出现了fail指针,为失配情况重新定位方案。
类似于next数组。
无解(定位不到失配后新方案),就指向根表示无解。
显而易见,首字母失配是一定没有方案的。
其次,一个字母失配可以定位到父节点失配的自己值子节点。
一个优化:没有新子节点的节点直接指向fail指针自己值子节点。
建出来Trie图是这样的:
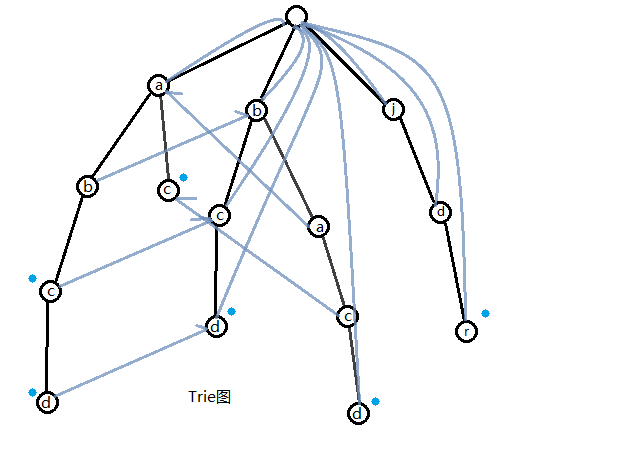
匹配时类似KMP:
模板代码(luogu P3808 【模板】AC自动机(简单版)):
1 #include<queue> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 struct trnt{ 6 int ch[26]; 7 int val; 8 int fl; 9 }tr[1000000]; 10 std::queue<int>Q; 11 char tmp[1000003]; 12 int siz; 13 int n; 14 void add(char *a) 15 { 16 int len=strlen(a+1); 17 int root=0; 18 for(int i=1;i<=len;i++) 19 { 20 int c=a[i]-'a'; 21 if(!tr[root].ch[c]) 22 tr[root].ch[c]=++siz; 23 root=tr[root].ch[c]; 24 } 25 tr[root].val++; 26 } 27 void Build() 28 { 29 int root=0; 30 for(int i=0;i<26;i++) 31 if(tr[root].ch[i]) 32 Q.push(tr[root].ch[i]); 33 while(!Q.empty()) 34 { 35 root=Q.front(); 36 Q.pop(); 37 for(int i=0;i<26;i++) 38 { 39 if(tr[root].ch[i]) 40 { 41 tr[tr[root].ch[i]].fl=tr[tr[root].fl].ch[i]; 42 Q.push(tr[root].ch[i]); 43 }else 44 tr[root].ch[i]=tr[tr[root].fl].ch[i]; 45 } 46 } 47 return ; 48 } 49 int Cal(char *a) 50 { 51 int len=strlen(a+1); 52 int ans=0; 53 int root=0; 54 for(int i=1;i<=len;i++) 55 { 56 int c=a[i]-'a'; 57 root=tr[root].ch[c]; 58 for(int j=root;j&&(tr[j].val!=-1);j=tr[j].fl) 59 { 60 ans+=tr[j].val; 61 tr[j].val=-1; 62 } 63 } 64 return ans; 65 } 66 int main() 67 { 68 scanf("%d",&n); 69 for(int i=1;i<=n;i++) 70 { 71 scanf("%s",tmp+1); 72 add(tmp); 73 } 74 Build(); 75 scanf("%s",tmp+1); 76 printf("%d ",Cal(tmp)); 77 return 0; 78 }