前序
四叉树或四元树也被称为Q树(Q-Tree)。四叉树广泛应用于图像处理、空间数据索引、2D中的快速碰撞检测、存储稀疏数据等,而八叉树(Octree)主要应用于3D图形处理。对游戏编程,这会很有用。本文着重于对四叉树与八叉树的原理与结构的介绍,帮助您在脑海中建立四叉树与八叉树的基本思想。本文并不对这两种数据结构同时进行详解,而只对四叉树进行详解,因为八叉树的建立可由四叉树的建立推得。若有不足之处,望能不吝指出,以改进之。^_^ 欢迎Email:zhanxinhang@gmail.com
四叉树与八叉树的结构与原理
四叉树(Q-Tree)是一种树形数据结构。四叉树的定义是:它的每个节点下至多可以有四个子节点,通常把一部分二维空间细分为四个象限或区域并把 该区域里的相关信息存入到四叉树节点中。这个区域可以是正方形、矩形或是任意形状。以下为四叉树的二维空间结构(左)和存储结构(右)示意图(注意节点颜 色与网格边框颜色):
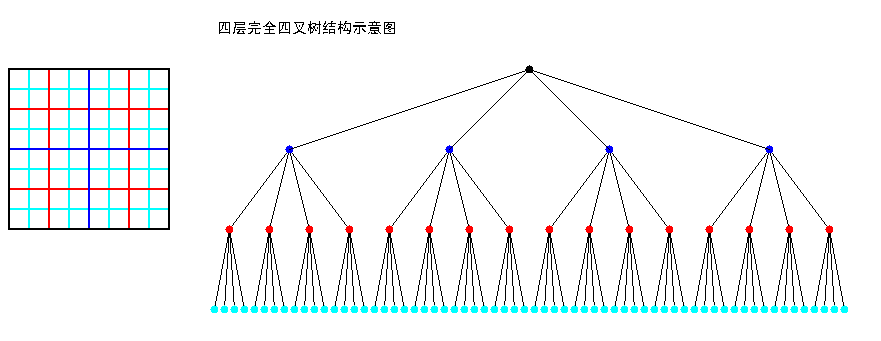
四叉树的每一个节点代表一个矩形区域(如上图黑色的根节点代表最外围黑色边框的矩形区域),每一个矩形区域又可划分为四个小矩形区域,这四个小矩形区域作为四个子节点所代表的矩形区域。
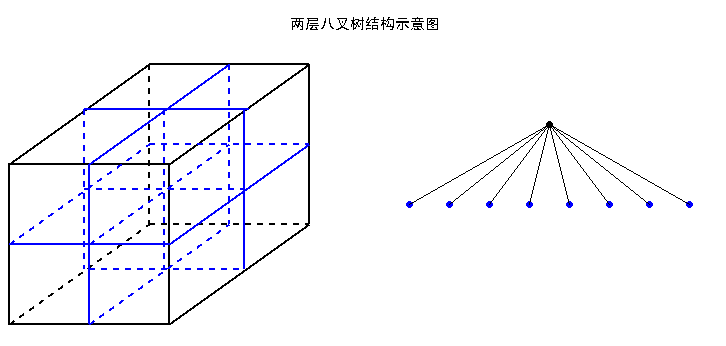
较之四叉树,八叉树将场景从二维空间延伸到了三维空间。八叉树(Octree)的定义是:若不为空树的话,树中任一节点的子节点恰好只会有八个,或零个,也就是子节点不会有0与8以外的数目。那么,这要用来做什么?想象一个立方体,我们最少可以切成多少个相同等分的小立方体?答案就是8个。如下八叉树的结构示意图所示:
四叉树存储结构的c语言描述:
- /* 一个矩形区域的象限划分::
- UL(1) | UR(0)
- ----------|-----------
- LL(2) | LR(3)
- 以下对该象限类型的枚举
- */
- typedef enum
- {
- UR = 0,
- UL = 1,
- LL = 2,
- LR = 3
- }QuadrantEnum;
- /* 矩形结构 */
- typedef struct quadrect_t
- {
- double left,
- top,
- right,
- bottom;
- }quadrect_t;
- /* 四叉树节点类型结构 */
- typedef struct quadnode_t
- {
- quadrect_t rect; //节点所代表的矩形区域
- list_t *lst_object; //节点数据, 节点类型一般为链表,可存储多个对象
- struct quadnode_t *sub[4]; //指向节点的四个孩子
- }quadnode_t;
- /* 四叉树类型结构 */
- typedef struct quadtree_t
- {
- quadnode_t *root;
- int depth; // 四叉树的深度
- }quadtree_t;
四叉树的建立
1、利用四叉树分网格,如本文的第一张图<四层完全四叉树结构示意图>,根据左图的网格图形建立如右图所示的完全四叉树。
伪码:
Funtion QuadTreeBuild ( depth, rect )
{
QuadTree->depth = depth;
/*创建分支,root树的根,depth深度,rect根节点代表的矩形区域*/
QuadCreateBranch ( root, depth, rect );
}
Funtion QuadCreateBranch ( n, depth,rect )
{
if ( depth!=0 )
{
n = new node; //开辟新节点
n ->rect = rect; //将该节点所代表的矩形区域存储到该节点中
将rect划成四份 rect[UR], rect[UL], rect[LL], rect[LR];
/*创建各孩子分支*/
QuadCreateBranch ( n->sub[UR], depth-1, rect [UR] );
QuadCreateBranch ( n->sub[UL], depth-1, rect [UL] );
QuadCreateBranch ( n->sub[LL], depth-1, rect [LL] );
QuadCreateBranch ( n->sub[LR], depth-1, rect [LR] );
}
}
2、假设在一个矩形区域里有N个对象,如下左图一个黑点代表一个对象,每个对象的坐标位置都是已知的,用四叉树的一个节点存储一个对象,构建成如下右图所示的四叉树。

方法也是采用递归的方法对该矩形进行划分分区块,分完后再往里分,直到每一个子矩形区域里只包含一个对象为止。
伪码:
Funtion QuadtreeBuild()
{
Quadtree = {empty};
For (i = 1;i<n;i++) //遍历所有对象
{
QuadInsert(i, root);//将i对象插入四叉树
}
剔除多余的节点; //执行完上面循环后,四叉树中可能有数据为空的叶子节点需要剔除
}
Funtion QuadInsert(i,n) //该函数插入后四叉树中的每个节点所存储的对象数量不是1就是0
{
if(节点n有孩子)
{
通过划分区域判断i应该放置于n节点的哪一个孩子节点c;
QuadInsert(i,c);
}
else if(节点n存储了一个对象)
{
为n节点创建四个孩子;
将n节点中的对象移到它应该放置的孩子节点中;
通过划分区域判断i应该放置于n节点的哪一个孩子节点c;
QuadInsert(i,c);
}
else if(n节点数据为空)
{
将i存储到节点n中;
}
}
(以上两种建立方法作为举一反三之用)
用四叉树查找某一对象
1、采用盲目搜索,与二叉树的递归遍历类似,可采用后序遍历或前序遍历或中序遍历对其进行搜索某一对象,时间复杂度为O(n)。
2、根据对象在区域里的位置来搜索,采用分而治之思想,时间复杂度只与四叉树的深度有关。比起盲目搜索,这种搜索在区域里的对象越多时效果越明显
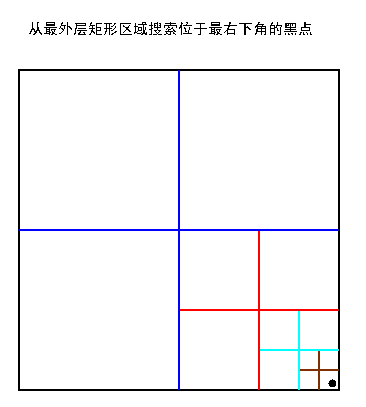
伪码:
Funtion find ( n, pos, )
{
If (n节点所存的对象位置为 pos所指的位置 )
Return n;
If ( pos位于第一象限 )
temp = find ( n->sub[UR], pos );
else if ( pos位于第二象限)
temp = find ( n->sub[UL], pos );
else if ( pos位于第三象限 )
temp = find ( n->sub[LL], pos );
else //pos 位于第四象限
temp = find ( n->sub[LR], pos );
return temp;
}
结语:
熟话说:结构之法,算法之道。多一种数据结构就多一种解决问题的方法,多一种方法就多一种思维模式。祝君学习愉快!^_^