常用排序算法实现

性能一览

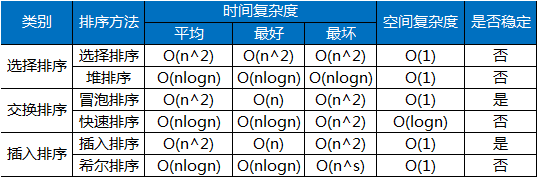
注释：

1. 稳定性：每趟排序完，会不会破坏元素的相对位置

2. 冒泡排序最好情况：O(n)，算法需要改进

3. 希尔排序：

1). 希尔排序的复杂度和增量序列是相关的
2). {1,2,4,8,...}这种序列并不是很好的增量序列，使用这个增量序列的时间复杂度（最坏情形）是O(n^2)

代码实现

public class Arithmetic {
    /**
     * 选择排序，升序排列
     *
     * @param nums
     * @return
     */
    public int[] selectSortArray(int[] nums) {
        for (int i = 0; i < nums.length - 1; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] > nums[j]) {
                    int temp = nums[i];
                    nums[i] = nums[j];
                    nums[j] = temp;
                }
            }
        }
        return nums;
    }

    /**
     * 冒泡排序，升序排列
     *
     * @param nums
     * @return
     */
    public int[] bubbleSortArray(int[] nums) {
        int len = nums.length;
        boolean didSwap;
        for (int i = 0; i < len - 1; i++) { //趟数
            didSwap = false;
            for (int j = 0; j < len - 1 - i; j++) { //次数
                if (nums[j] > nums[j + 1]) {
                    int temp = nums[j];
                    nums[j] = nums[j + 1];
                    nums[j + 1] = temp;

                    didSwap = true;
                }
            }

            if(!didSwap) {
                return nums;
            }
        }
        return nums;
    }

    /**
     * 快速排序，升序排列
     *
     * @param nums
     * @return
     */
    public int[] quickSortArray(int[] nums) {
        partitionQuickSort(0, nums.length - 1, nums);
        return nums;
    }

    private void partitionQuickSort(int low, int high, int[] nums) {
        if (low >= high) return;
        int lowTemp = low;
        int highTemp = high;
        int tempNum = nums[lowTemp];

        while (lowTemp < highTemp) {
            while (nums[highTemp] >= tempNum &&
                    lowTemp < highTemp) {
                highTemp--;
            }

            if (lowTemp == highTemp) {
                break;
            }

            nums[lowTemp] = nums[highTemp];
            lowTemp++;
            
            while (nums[lowTemp] <= tempNum &&
                    lowTemp < highTemp) {
                lowTemp++;
            }

            if (lowTemp == highTemp) {
                break;
            }

            nums[highTemp] = nums[lowTemp];
            highTemp--;
        }

        //给中间的赋值
        nums[lowTemp] = tempNum;

        partitionQuickSort(low, lowTemp - 1, nums);
        partitionQuickSort(highTemp + 1, high, nums);
    }

    /**
     * 插入排序，升序排列
     *
     * @param nums
     * @return
     */
    public int[] insertSortArray(int[] nums) {
        for (int i = 1; i < nums.length; i++) {
            int index = i - 1;
            int insertVal = nums[i];

            while (index >= 0 && insertVal < nums[index]) {
                nums[index + 1] = nums[index];
                index--;
            }

            nums[index + 1] = insertVal;
        }

        return nums;
    }

    /**
     * 希尔排序, 升序排列
     *
     * @param nums
     * @return
     */
    public int[] shellSortArray(int[] nums) {
        int gap = nums.length;
        do {
            gap = (gap + 1) / 2;
            for (int i = gap; i < nums.length; i++) {
                int index = i - gap;
                int insertVal = nums[i];

                while (index >= 0 && insertVal < nums[index]) {
                    nums[index + gap] = nums[index];
                    index -= gap;
                }

                nums[index + gap] = insertVal;
            }
        } while (gap > 1);
        return nums;
    }

}

参考：
https://blog.csdn.net/yushiyi6453/article/details/76407640
https://blog.csdn.net/qq_39207948/article/details/80006224