拉格朗日插值

1. 问题：给出(n)个点(P_{i}(x_i,y_i))，将过这(n)个点的最多(n-1)次的多项式记为(f(x))，求(f(k))的值。
   普通做法：(O(n^2 + n^3 + n))列方程 + 高斯消元求解 + 秦玖韶算法求值
   时间复杂度爆炸，还不好写
   接下来说说拉格朗日插值
2. 拉格朗日插值
   数学上来说，拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。

• 我们来看看如何认识拉格朗日插值
  若知道(3)个点，想要得到一根曲线通过这(3)个点，一定得是(2)次多项式
  第一根曲线(f_1(x))，在(x_1)点处，取值为1，其余两点取值为0：
                                                              
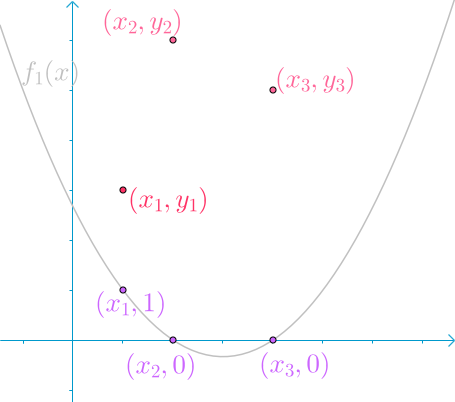
  第二根曲线(f_2(x))，在(x_2)点处，取值为(1)，其余两点取值为(0)：
                                                              
  第三根曲线(f_3(x))，在(x_3)点处，取值为(1)，其余两点取值为(0)：
                                                              
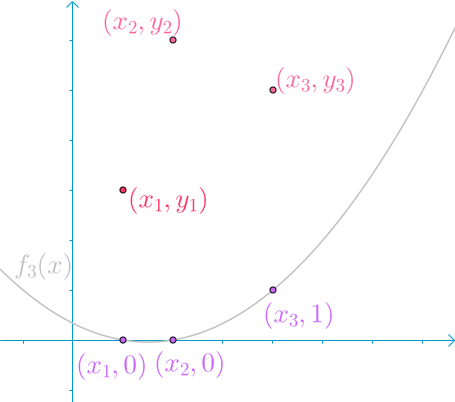
  这三根曲线可以保证待求曲线一定经过这三个点
  (y_1f_1(x))可以保证，在(x_1)点处，取值为(y_1)，其余两点取值为(0)。
  (y_2f_2(x))可以保证，在(x_2)点处，取值为(y_2)，其余两点取值为(0)。
  (y_3f_3(x))可以保证，在(x_3)点处，取值为(y_3)，其余两点取值为(0)。
  那么：

[f(x) = y_1f_1(x_1) + y_2f_2(x_2) + y_3f_3(x_3) ]

        可以穿过这三个点
                                                            

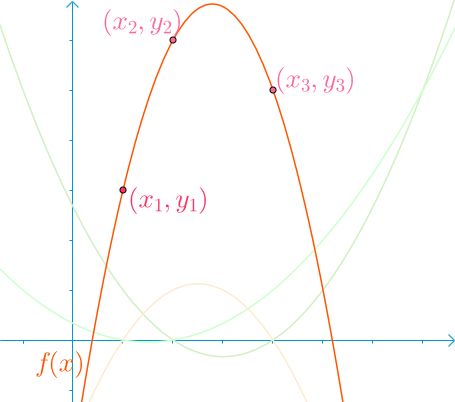
• 严谨一点的证明
  我们构造符合如下条件的二次函数

[ f_i(x_j)=left{ egin{aligned} 1 ~~ i = j \ 0 ~~ i ot= j end{aligned} ight. ]

[f_i(x) = prod_{j ot= i}^{1 le j le 3}frac{x-x_j}{x_i - x_j} ]

        于是$$f(x) = sum_{i = 1}^{3}y_if_i(x)$$
        更一般的：

[f(x) = sum_{i = 1}^{n}y_if_i(x) ]

        这就是拉格朗日插值的一般形式
3. 放一下代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4;
const int Mod = 998244353;
int n,k;
int x[N],y[N];

int Fastmi(int a,int b)
{
	int ans = 1 % Mod;
	for(;b;b >>= 1)
	{
		if(b & 1)
		{
			ans = (long long)ans * a % Mod;
		}
		a = (long long)a * a % Mod;
	}
	return ans;
}

int main()
{
	cin >> n >> k;
	for(int i = 1;i <= n;i ++ )
	{
		cin >> x[i] >> y[i];
	}
	
	long long ans = 0;
	for(int i = 1;i <= n;i ++ )
	{
		long long s1 = 1,s2 = 1;
		for(int j = 1;j <= n;j ++ )
		{
			if(i != j)
			{
				s1 = 1ll * s1 * (k - x[j]) % Mod;
				s2 = 1ll * s2 * (x[i] - x[j]) % Mod;
			}
		}
		ans = (1ll * ans + 1ll * y[i] * s1 % Mod * Fastmi(s2,Mod - 2) % Mod) % Mod;
	}
	cout << (ans + Mod) % Mod << endl;
	return 0;
}

借用了知乎答主的回答和照片，他讲的实在太好了