Ordering Tasks UVA

在一个有向图中，对所有的节点进行排序，要求没有一个节点指向它前面的节点。

先统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向的节点的入度减一。

一直做改操作，直到所有的节点都被分离出来。

如果最后不存在入度为0的节点，那就说明有环，不存在拓扑排序，也就是很多题目的无解的情况。

下面是算法的演示过程。

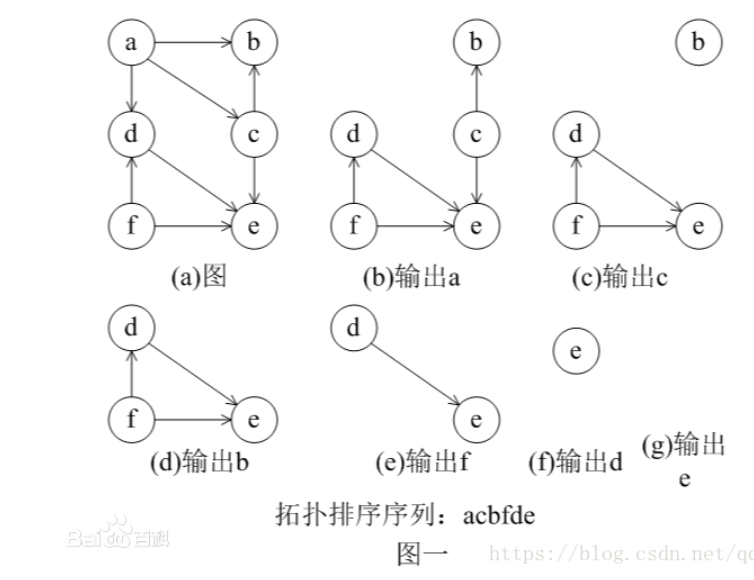
下面看一道例题

题目链接：https://vjudge.net/problem/UVA-10305

代码真的很简单 ，完全是水题。

 看代码：

#include<iostream>
#include<queue>
#include<vector>
#include<string.h>
using namespace std;
const int maxn=100+5;
int N,M;
int in[maxn];//表示该节点的入度
int edge[maxn][maxn];//edge[i][j]不为0表示i到j有路

void solve()
{
    queue<int> q;
    vector<int>ans;
    for(int i=1;i<=N;i++)
    {
        if(in[i]==0) q.push(i);//入度为0的结点入队列
    }
    while(!q.empty())
    {
        int p=q.front();
        q.pop();
        ans.push_back(p);//拿出入度为0的结点
        for(int i=1;i<=N;i++)//与该结点之间有边的入度减1
        {
            if(edge[p][i])
            {
                edge[p][i]--;
                in[i]--;
                if(in[i]==0) q.push(i);//入度减为0  入队列
            }

        }
    }
    cout<<ans[0];
    for(int i=1;i<ans.size();i++) cout<<" "<<ans[i];
    cout<<endl;
    return ;
}
int main()
{

    int a,b;
    while(cin>>N>>M)
    {
        if(N==0&&M==0) break;
        memset(edge,0,sizeof(edge));
        memset(in,0,sizeof(in));
        for(int i=0;i<M;i++)
        {
            cin>>a>>b;
            in[b]++;
            edge[a][b]++;
        }
        solve();
    }

    return 0;
}