这道题题意描述很清楚,不过我自己做的时候确实是一头雾水……又看了题解,发现要用到一个新知识,叫purfer序列。
我们来简单说一下什么是purfer序列。它可以被看作一种树的表现形式。一棵含有n个节点的树可以用一个长度为n-2的purfer序列表示,而其中每一个树都是1~n之间的一个数。
每一棵树,它都有自己唯一的purfer序列,反过来,对于每一个purfer序列,都能获得唯一的一棵树。也就是说,树与其purfer序列一一对应。
先说一下怎么求purfer序列。首先找出这棵树中,节点编号数最小的一个叶子结点(度数为1,只有连向其父亲的一条边),把与它相连的那个节点加入到purfer序列中,并且将这个节点和与之相连的边从这棵树中删除。重复上述过程n-2步,得到一个长度为n-2的purfer序列和一个只有两个节点的树。
(还是偷一下大神的图来描述这件事)
看看下面的例子:
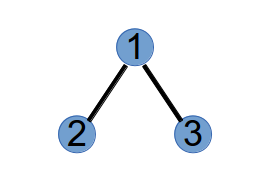
假设有一颗树有 5 个节点,四条边依次为:(1, 2), (1, 3), (2, 4), (2, 5),如下图所示:
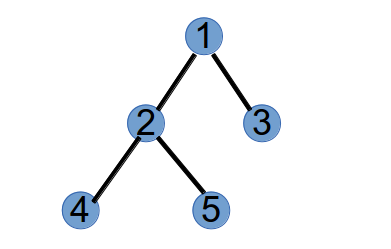
第 1 步,选取具有最小标号的叶子节点 3,将与它相连的点 1 作为第 1 个 Purfer Number,并从树中删掉节点 3:
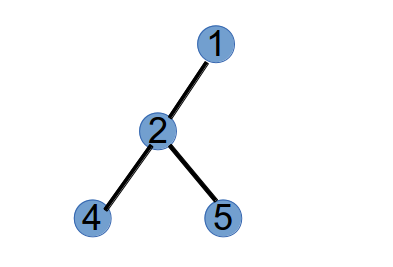
第 2 步,选取最小标号的叶子节点 1,将与其相连的点 2 作为第 2 个 Purfer Number,并从树中删掉点 1:
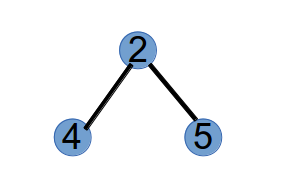
第 3 步,选取最小标号的叶子节点 4,将与其相连的点 2 作为第 3 个 Purfer Number,并从树中删掉点 4:
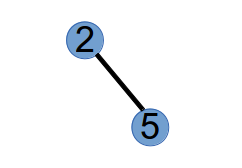
最后,我们得到的 Purfer Sequence 为:1 2 2
既然如此,purfer序列就求好了,那我们再说一下怎么通过purfer序列求它相对应的树。
先把所有节点的度数赋为1,再加上其在Purfer序列中出现过的次数,得到每一个节点的度。每次选取编号最小的度数为1的节点(比如当前枚举到第i个点),将这个节点和Purfer序列中第i个数所对应的点连一条边,并且把这两个点的度数-1。最后得到两个度数为1的点,我们再把他们连边,加入到树中。这样就成功的通过purfer序列求出一棵树了。
(我们再偷一次大神的图并且以上面的例子为例描述一下这个过程)(感谢大神orz)
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 2 | 3 | 1 | 1 | 1 |
第 1 次执行,选取最小标号度为 1 的点 3 和 Purfer Sequence 中的第 1 个数 1 连边:

将 1 和 3 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 1 | 3 | 0 | 1 | 1 |
第 2 次执行,选取最小标号度为 1 的点 1 和 Purfer Sequence 中的第 2 个数 2 连边:
将 1 和 2 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 0 | 2 | 0 | 1 | 1 |
第 3 次执行,将最小标号度为 1 的点 4 和 Purfer Sequence 第 3 个数 2 连边:

将 2 和 4 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 0 | 1 | 0 | 0 | 1 |
最后,还剩下两个点 2 和 5 的度为 1,连边:
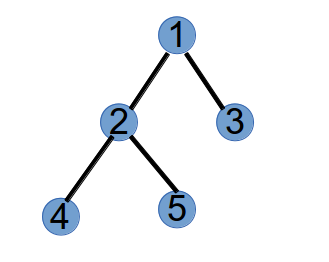
这样我们就知道,purfer序列必然与树是一一对应的。
而且我们还知道了一条性质,一个点在purfer序列中出现的次数等于其度数-1.
那我们来看一下这道题。
首先考虑无解的情况,这个很好判断,如果任意一个点的度数是0或者大于n-1那么就无解,否则有解。
之后再看一般的情况。我们假设一共有m个节点是有度数限制的,剩下n-m个节点没有度数限制。那么sum = sigma 1~m(d[i] - 1)
也就是说,这些点占据了purfer序列中sum个位置(一共有n-2个位置),所以这次选择的种类是C(n-2,sum)
之后对于这个长度为sum的序列,我们考虑一下,第一个位置可以填入d[1]-1个数,选择的方案为C(sum,d[1]-1),那么在第二个位置可以填d[2]-1个数,选择的方案就是C(sum-(d[1]-1),d[2]-1)。
这样推下去,可以得到总的排列数是:(偷一下图吧(^_^))

之后,因为剩下的n-2-sum个位置,每个没有度数限制,所以可以随便填,那么就还有m^(n-2-sum)种情况。把两者相乘即为答案。
不过写高精度是不可能的。
我们可以对每个元素都进行质因数分解,开个桶记录一下每个数的出现次数,最后把他们乘起来就好。可以先行约去分子分母中相同的数。
不过最后一波把所有数乘起来还是要高精的……不过反正是高精乘低精,比较好写。
写题的时候还有个小插曲……质因数分解的时候,非常智障的写成了while(p),结果导致出现了floating point exception :8这么个错误(好像在Windows下是RE)
不管怎么说,以后要注意啊。
上一下代码。(这题其实很神奇因为不需要求puffer序列)
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cmath> #include<queue> #include<set> #define rep(i,a,n) for(int i = a;i <= n;i++) #define per(i,n,a) for(int i = n;i >= a;i--) #define enter putchar(' ') using namespace std; const int M = 10005; int n,len,a,sum,k,tot; int t[10001],ans[M+1],prime[M+1]; bool np[M]; int read() { int ans = 0,op = 1; char ch = getchar(); while(ch < '0' || ch > '9') { if(ch == '-') op = -1; ch = getchar(); } while(ch >='0' && ch <= '9') { ans *= 10; ans += ch - '0'; ch = getchar(); } return ans * op; } void euler() { rep(i,2,n) { if(!np[i]) prime[++tot] = i; for(int j = 1;i * prime[j] <= n;j++) { np[prime[j] * i] = 1; if(!(i % prime[j])) break; } } } void C(int a,int b) { rep(i,b+1,a) { int p = i,d = 1; while(p > 1) { while (!(p % prime[d])) ans[d]++,p /= prime[d]; d++; } } rep(i,1,a-b) { int p = i,d = 1; while(p > 1) { while (!(p % prime[d])) ans[d]--,p /= prime[d]; d++; } } } void calc() { int d = 1; while(sum > 1) { while (!(sum % prime[d])) ans[d] += len,sum /= prime[d]; d++; } } int main() { n = read(); euler(); len = n-2; rep(i,1,n) { a = read(); if(!a || a >= n) { printf("0"); return 0; } if(a == -1) { sum++; continue; } a--,C(len,a),len -= a; } if(len) calc(); t[1] = 1,k = 1; rep(i,1,170) { while(ans[i]) { ans[i]--; rep(j,1,k) t[j] *= prime[i]; rep(j,1,k) if(t[j] >= 10) t[j+1] += t[j]/10,t[j] %= 10; while(t[k+1]) k++,t[k+1] += t[k] / 10,t[k] %= 10; } } per(i,k,1) printf("%d",t[i]); enter; return 0; }