判断平面的一堆点是否在两条直线上

D. Pair Of Lines

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given n points on Cartesian plane. Every point is a lattice point (i. e. both of its coordinates are integers), and all points are distinct.

You may draw two straight lines (not necessarily distinct). Is it possible to do this in such a way that every point lies on at least one of these lines?

Input

The first line contains one integer n (1 ≤ n ≤ 10⁵) — the number of points you are given.

Then n lines follow, each line containing two integers x_i and y_i (|x_i|, |y_i| ≤ 10⁹)— coordinates of i-th point. All n points are distinct.

Output

If it is possible to draw two straight lines in such a way that each of given points belongs to at least one of these lines, print YES. Otherwise, print NO.

Examples

Input

Copy

5
0 0
0 1
1 1
1 -1
2 2

Output

YES

Input

Copy

5
0 0
1 0
2 1
1 1
2 3

Output

NO

Note

In the first example it is possible to draw two lines, the one containing the points 1, 3 and 5, and another one containing two remaining points.

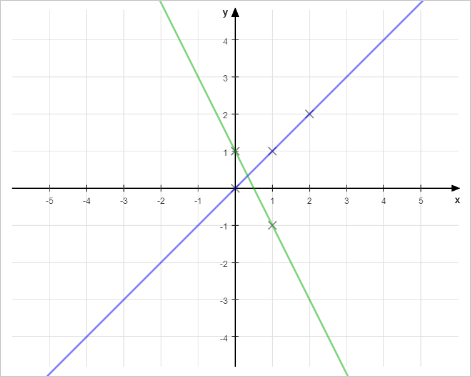
题意 ： 给定平面的一些点，问是否最多用两条直线去描绘出这些点。

思路分析 ： 对于平面一堆点中的任意3个，若其可以用两条直线去表示，则一定 1 3 或者 2 3 或者 1 2 是在一起的。那么就根据这个去判断每个点就行。

注意斜率 ！ 判断两个斜率是否相等的时候需要用乘的关系去判断，除的关系去判断时若斜率不存在时，则会出现问题，分母为 0 了

注意 long long

代码示例 ：

#define ll long long
const ll maxn = 1e5+5;
const double pi = acos(-1.0);
const ll inf = 0x3f3f3f3f;

ll n;
struct node
{
    ll x, y;
}pre[maxn];
bool vis[maxn];

bool fun(node a, node b, node c){
    ll k1 = (b.y-a.y)*(c.x-a.x);
    ll k2 = (c.y-a.y)*(b.x-a.x);
    return k1==k2?true:false;
}

bool check(ll a, ll b){
    
    memset(vis, false, sizeof(vis));
    vis[a] = vis[b] = true;
    
    for(ll i = 1; i <= n; i++){
        if (i == a || i == b) continue;
        if (fun(pre[a], pre[b], pre[i])) vis[i] = true;
    }
    ll p1=-1, p2=-1;
    for(ll i = 1; i <= n; i++){
        if (!vis[i]){
            if(p1 == -1) {p1=i;}
            else if (p2==-1){p2=i;}
        }
    }
    if (p1==-1||p2==-1) return true;
    for(ll i = 1; i <= n; i++){
        if (i == p1 || i == p2) continue;
        if (!vis[i] && !fun(pre[p1], pre[p2], pre[i])) return false;
    }
    return true;
}

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    cin >> n;
    for(ll i = 1; i <= n; i++){
        scanf("%lld%lld", &pre[i].x, &pre[i].y);        
    }
    if (n < 5 || check(1, 2) || check(1, 3) || check(2, 3)){
        printf("YES
");
    }
    else printf("NO
");
    return 0;
}