sklearn.svm 支持向量机

 

一、基本概念

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。支持向量机(Support Vector Machine：SVM)的目的是用训练数据集的间隔最大化找到一个最优分离超平面

二、模型原理

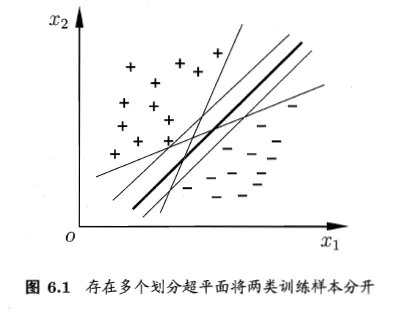
在给定的训练样本，找到一个超平面将不同类别的样本分开

1.超平面的公式如下：

其中，ω= (ω1,ω2...ωn) 为法向量，决定了超平面的方向，b是位移向，决定了超平面和原点之间的距离

2.样本到超平面的距离，样本空间中任意点x到超平面（记为（ω,b））的距离：

3.约束条件和支持向量机（support vector）

式(6.3)即为超平面将训练样本正确分类的约束条件。如下图所示，距离超平面最近的三个训练样本使得式(6.3)的等号成立，它们就是支持向量

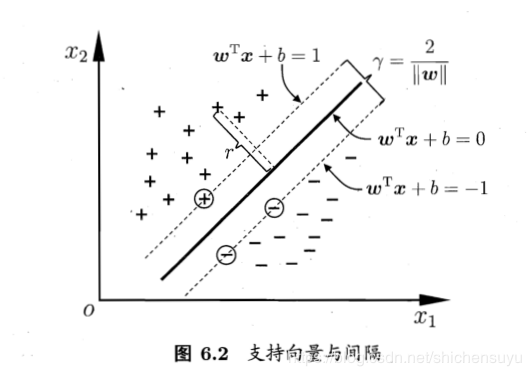
4.间隔(margin)：两个不同类别的支持向量分别到超平面的距离之和

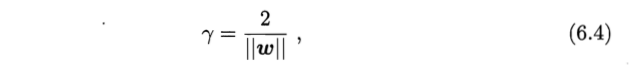
 最优的划分超平面需要使得间隔 r 最大化

 

这就是支持向量机的基本型

下面的是（6.2）和（6.3）的推导

 

 

 

 https://blog.csdn.net/shichensuyu/article/details/90678747

支持向量机的优势：

（1）在高维空间非常高效

（2）即使在数据维度比样本数量大的情况下仍然有效

（3）在决策函数（称为支持向量）中使用训练集的子集,因此它也是高效利用内存的

（4）通用性: 不同的核函数 核函数 与特定的决策函数一一对应.常见的 kernel 已经提供,也可以指定定制的内核

支持向量机缺点：

（1）如果特征数量比样本数量大得多,在选择核函数 核函数 时要避免过拟合, 而且正则化项是非常重要的

（2）支持向量机不直接提供概率估计,这些都是使用昂贵的五次交叉验算计算的