study from :
https://www.cnblogs.com/peng-ym/p/9446555.html
study later:

之后再说……
(from https://www.luogu.org/problemnew/solution/P5325)
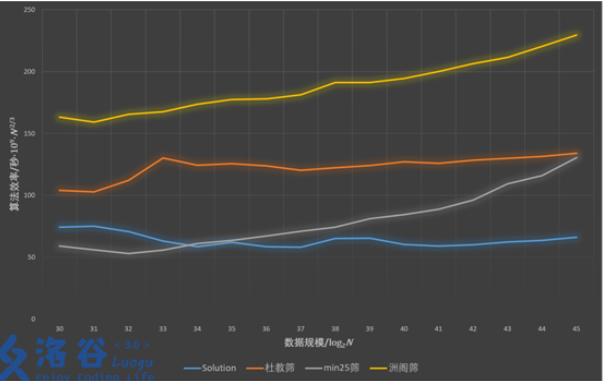
基础公式

一般套路
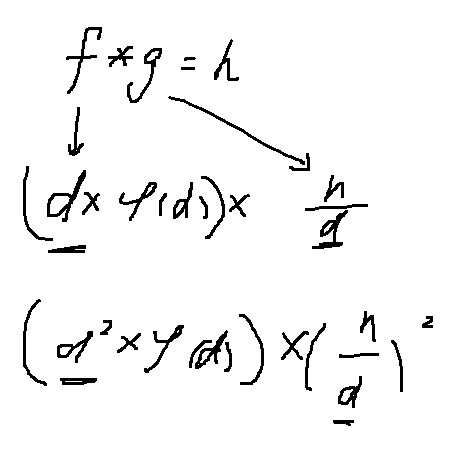
莫比乌斯反演

n的约数中,系数为1的公因数,
可以选择或不选择,
u(d)=最终选择的个数 奇 -1 ; 偶 1
总的情况数 2^k
唯有k=0,才不对称,使最终结果为1
欧拉函数
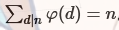

其中一个容易想到的方法是数学归纳法。
d=x*y
其中y是质数
通过 (x)和
(x)和 (y)推出
(y)推出 (xy)。
(xy)。
luogu4213
https://www.luogu.org/problemnew/show/P4213
在内存不超限的情况下,预处理更多的项
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cmath> 4 #include <cstring> 5 #include <string> 6 #include <algorithm> 7 #include <iostream> 8 using namespace std; 9 #define ll long long 10 #include <unordered_map> 11 12 const double eps=1e-8; 13 const ll inf=1e9; 14 const ll mod=1e9+7; 15 const int maxn=1e7+10; 16 17 ///unordered_map rather than map, faster 在寻找上,unordered_map优于map 18 unordered_map<int,ll>ma1; 19 unordered_map<int,int>ma2; 20 int maxv=5e6;///maxv较大的时候,v1,v2是否会超int 21 //int maxv=10; 22 bool vis[maxn]; 23 int v2[maxn],zhi[maxn],zhi_cnt; 24 ll v1[maxn]; 25 26 void init() 27 { 28 int i,j,k; 29 v1[1]=v2[1]=1; 30 for (i=2;i<=maxv;i++) 31 { 32 if (!vis[i]) 33 { 34 zhi[++zhi_cnt]=i; 35 v1[i]=i-1; 36 v2[i]=-1; 37 } 38 for (j=1;j<=zhi_cnt;j++) 39 { 40 k=i*zhi[j]; 41 if (k>maxv) 42 break; 43 vis[k]=1; 44 if (i%zhi[j]==0) 45 { 46 v1[k]=v1[i]*zhi[j]; 47 break; 48 } 49 else 50 v1[k]=v1[i]*(zhi[j]-1); 51 v2[k]=-v2[i]; 52 } 53 } 54 for (i=1;i<=maxv;i++) 55 { 56 v1[i]+=v1[i-1]; 57 v2[i]+=v2[i-1]; 58 } 59 } 60 61 ll cal1(int n) 62 { 63 if (n<=maxv) 64 return v1[n]; 65 if (ma1.find(n)!=ma1.end()) 66 return ma1[n]; 67 int l,r; 68 ll sum=1ll*n*(n+1)/2; 69 ///N<=2^31-1 存在被卡的可能,l=2^31-1+1 70 ///n=1时,要特判 71 for (l=2,r=0;r!=n;l=r+1) 72 { 73 r=n/(n/l); 74 sum-=cal1(n/l)*(r-l+1); 75 } 76 ma1[n]=sum; 77 return sum; 78 } 79 80 int cal2(int n) 81 { 82 if (n<=maxv) 83 return v2[n]; 84 if (ma2.find(n)!=ma2.end()) 85 return ma2[n]; 86 int l,r; 87 int sum=1; 88 for (l=2,r=0;r!=n;l=r+1) 89 { 90 r=n/(n/l); 91 sum-=cal2(n/l)*(r-l+1); 92 } 93 ma2[n]=sum; 94 return sum; 95 } 96 97 int main() 98 { 99 int t,n; 100 init(); 101 scanf("%d",&t); 102 while (t--) 103 { 104 scanf("%d",&n); 105 printf("%lld %d ",cal1(n),cal2(n)); 106 } 107 return 0; 108 }
(from https://www.cnblogs.com/peng-ym/p/9446555.html)
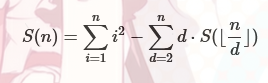
等差数列形式
1 int n,l,r; 2 ll sum=0; 3 for (l=2;l<=n;l=r+1) 4 { 5 r=n/(n/l); 6 sum+=(l+r)*(r-l+1)/2*value[n/l]; 7 }
其它题目:
luogu3768 简单的数学题
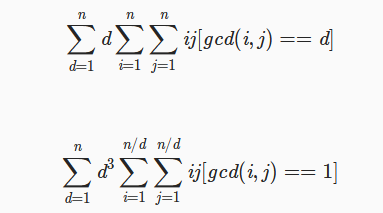
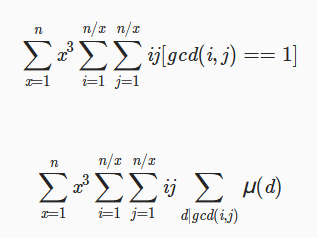
BZOJ 4916 神犇和蒟蒻
……