防止遗忘,好记性不如烂博文(雾
线段树
这年头怎么在哪儿码题都能碰到这玩意儿
线段树(( ext{Segment tree}))可谓是 ( ext{OIer}) 们的家常便饭,应用于维护区间信息(需满足结合律)。另外别跟我拿树状数组和它比。
从小见大,边看题边学习~
维护区间和
(洛谷 ( ext{P3372}) 【模板】线段树 ( ext{1}))
题目描述
已知一个数列,你要进行下面两种操作:
- 将某区间每一个数加上 ( ext{x})。
- 求出区间和。
输入格式
第一行包含两个整数 ( ext{n, m}),分别表示该数列数字的个数和操作的总个数。
第二行包含 ( ext{n}) 个用空格分隔的整数,其中第 ( ext{i}) 个数字表示数列第 ( ext{i}) 项的初始值。
接下来 ( ext{m}) 行每行包含 ( ext{3}) 或 ( ext{4}) 个整数,表示一个操作,具体如下:
操作 ( ext{1}): 格式:( ext{1 x y k}) 含义:将区间 ( ext{[x,y]}) 内每个数加上 ( ext{k})。
操作 ( ext{2}): 格式:( ext{2 x y}) 含义:输出区间 ( ext{[x,y]}) 内每个数的和。
输出格式
输出包含若干行整数,即为所有操作 ( ext{2}) 的结果。
基本的建树
线段树是一棵平衡二叉树,根节点维护全区间,然后往下对半分(即每个节点都存了条线段)。不保证所有的区间都是线段树的节点。当然还要依题存区间和啊什么的值。
编号为 ( ext{k}) 的节点,左右儿子节点编号分别为 ( ext{k << 1, k << 1 | 1}),若节点 ( ext{k}) 存储区间 ( ext{[l,r]}) 的和,则左右儿子节点分别存储区间 ( ext{[l, mid]}) 和 ( ext{mid + 1, r}) 的和,其中 ( ext{mid = l + r >> 1}),左节点存储区间长度,与右节点相同或多 ( ext{1})。
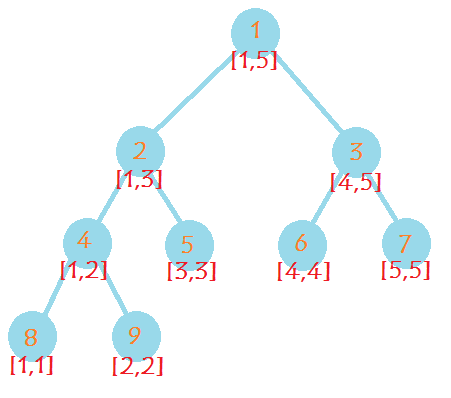
递归建立线段树:
void build (int l, int r, int p) {
if (l == r) { // 叶子结点
t[p] = a[l]; // 直接取数组值
return ;
}
int mid = l + r >> 1;
build (l, mid, p << 1);
build (mid + 1, r, p << 1 | 1); // 建立儿子节点
t[p] = t[p << 1] + t[p << 1 | 1]; // 本节点值为儿子节点和
}
区间修改
引入懒标记,朴素想法为使用递归一层层修改,但复杂度较高。使用懒标记后,对于恰好是线段树节点的区间,直接打上标记,不用递归,等用到他的子区间时,向下传递。
void upd (int cl, int cr, int d, int p = 1, int l = 1, int r = n) {
// 参数意义:最初修改的区间,修改值,当前分出来的区间所在的节点
if (l > cr or r < cl) { // 区间无交集
return ;
}
if (l >= cl and r <= cr) {
// 直接在区间节点上加,其实换成 == 没影响
t[p] += (r - l + 1) * d;
if (r > l) tag[p] += d;
return ;
}
int mid = l + r >> 1;
tag[p << 1] += tag[p]; // 传递标记
tag[p << 1 | 1] += tag[p];
t[p << 1] += tag[p] * (mid - l + 1);
t[p << 1 | 1] += tag[p] * (r - mid); // 向下更新
tag[p] = 0; // 清除标记
upd (cl, cr, d, p << 1, cl, mid);
upd (cl, cr, d, p << 1 | 1, mid + 1, r); // 重复步骤,继续向下更新
t[p] = t[p << 1] + t[p << 1 | 1]; //更新当前节点
}
中间有一段常被习惯性地封装:
inline void push_down (int p, int len) {
tag[p << 1] += tag[p]; // 传递标记
tag[p << 1 | 1] += tag[p];
t[p << 1] += tag[p] * (len - len / 2);
t[p << 1 | 1] += tag[p] * (len / 2); // 向下更新
tag[p] = 0; // 清除标记
}
然后直接在 ( ext{upd}) 函数里调用:
push_down (p, r - l + 1);
单点修改。。。让修改区间左右端点相等即可。
区间查询
跟上面差不多
int query (int ql, int qr, int p = 1, int l = 1, int r = n) {
if (l > qr or r < ql) return ;
if (ql <= l and qr >= r) return t[p];
int mid = l + r >> 1;
push_down (p, r - l + 1);
return query (ql, qr, p << 1, l, mid) +
query (ql, qr, p << 1 | 1, mid + 1, r);
}
没了。
实际上线段树还可以维护区间最值、区间 ( ext{gcd}) 等等,操作除了区间加也可以是区间乘、区间赋值,了解原理后很容易改。
主席树
真名其实是可持久化线段树,之所以叫它主席树。。。
由于发明者黄嘉泰姓名的缩写与前中共中央***、国家主席(已被博客园和谐)(H.J.T.)相同,因此这种数据结构也可被称为***树或主席树。
From Wikipedia.org
可持久化意思是我们可访问历史版本。
(关于文中的代码,由于我自己并没有将代码编译运行所以不保证它们是对的,如有错误欢迎帮忙指正)
主席树结构
主席树支持查询历史版本(每次操作都会使版本更新)。传统的暴力思路是每次操作都进行一次备份,但毫无疑问 ( ext{MLE}),所以只好利用某种方法进行压缩。
下面我们从小问题入手,先思考一棵单点修改区间查询的线段树的可持久化方法。
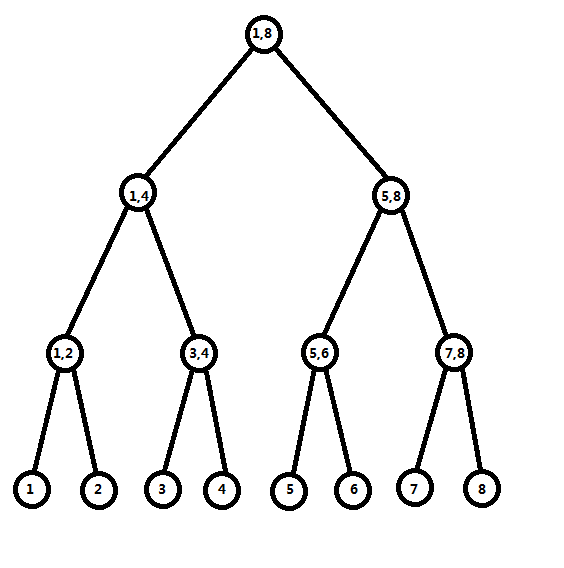
此时对下标为 ( ext{3}) 的节点进行操作,如何产生新版本,并保留旧版本?
众所周知,操作单点最多会使线段树的 ( ext{log n}) 个节点被修改,那么考虑这 ( ext{log n}) 个节点。我们动态开点,修改 ( ext{3}),并把经过的点全部拷贝一份,然后把空的左右儿子连到原本的地方。
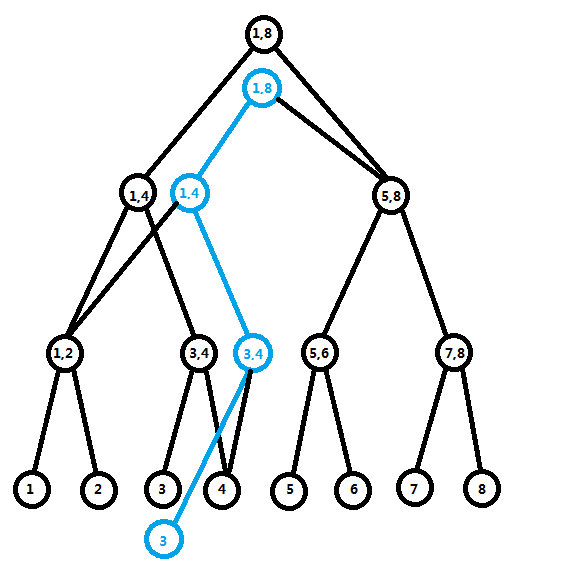
差不多就跟分层图一样。
这样每次操作最多开 ( ext{log n}) 个节点,若有 ( ext{k}) 次操作,则空间也就 ( ext{n long n + k log n})。
以下是示例代码:
#define N 100010
#define ls(x)
#define rs(x)
#define mid (l + r >> 1)
struct blanc {
int ls, rs, sum;
} t[N << 4]; // 这里请注意空间大小
int a[N], tot;
int build (int l, int r) {
int x = ++tot;
if (l == r) return x;
t[x].ls = build (l, mid);
t[x].rs = build (mid + 1, r);
return x;
}
/* 下面的 update 函数与平常的线段树略有不同 */
int upd (int k, int l, int r, int pre, int w) {
int x = ++tot;
/* 复制信息 */
t[x] = t[pre];
/* 新版本更新 */
t[x].sum += w;
if (l == r) return x;
if (k <= mid) t[x].ls = upd (k, l, mid, t[pre].ls, w);
else t[x].rs = upd (k, mid + 1, r, t[pre].rs, w);
return x;
}
用武之地
区间第 k 小问题
我们维护数字出现次数的前缀和,然后复刻权值线段树的操作,顺着次数的大小关系找出第 ( ext{k}) 大(其实是大还是小都是一样的做法),代码如下:
int query (int l, int r, int pre, int now, int k) {
int w = sum[t[now].ls] - sum[t[pre].ls];
if (l == r) return l;
if (k <= w) return query (l, mid, t[pre].ls, t[now].ls, k);
return query (mid + 1, r, t[pre].rs, t[now].rs, k - w);
}
排列的区间交集
当然在离散化的前提下,不是排列也能给他变成排列(bushi
我们设有排列 ( ext{A|1 - n|}) 和排列 ( ext{B|1 - m|})。
将 ( ext{A}) 中的数字的出现位置记下,( ext{pos[A[i]] = i}),然后将 ( ext{B}) 放入主席树进行维护。每次将 ( ext{B}) 中的数字按顺序,以 ( ext{pos[B[i]]}) 为坐标放入主席树。在回答 ( ext{A[l - r]}cap ext{B[L - R]}) 时,用 ( ext{R}) 版本查询 ( ext{[l - r]}) 的数字出现次数前缀和,减去 ( ext{L - 1}) 版本查询 ( ext{[l - r]}) 的数字出现次数前缀和,即可知两端区间交集元素个数。
int query (int ql, int qr, int l, int r, int p) {
if (ql <= l and r <= qr) return t[p].sum;
int mid = (l + r) >> 1, ans = 0;
if (ql <= mid) ans = query (ql, qr, l, mid, t[p].ls);
if (mid < qr) ans += query (ql, qr, mid + 1, r, t[p].rs);
return ans;
}
inline int inquire (int l1, int r1, int l2, int r2) {
return query (l1, r1, 1, n, rt[r2]) - query (l1, r1, 1, n, rt[l1 - 1]);
}
inline void build (int a[], int b[], int n, int m) {
int pos[n];
for (int i = 1; i <= n; i++) pos[a[i]] = i;
for (int i = 1; i <= m; i++) rt[i] = upd (pos[b[i]], 1, n, rt[i - 1], 1);
}