FFT,NTT入门

目录

• -1.前置知识
  • 复数
  • 单位根
  • 单位根反演
• 0.卷积
• 1.FFT

-1.前置知识

复数

  复数单位(i)：定义为(i^2=-1)。(i)可以直接参与运算。
  复数：形如(z=a+bi)的数被称为复数，其中(a)称为实部，(b)称为虚部。可以发现，当(b=0)的时候，(z)就是实数。
  复平面：建立直角坐标系。对于复数(z=a+bi)，其在复数平面上的坐标就是((a,b))；即横轴表示实部，纵轴表示虚部。另外，一个复数同样可以被表示为复平面上的一个从原点出发的向量。
  复数的运算：设(x=a+bi,y=c+di)，定义如下：
    (x+y=a+bi+c+di=(a+c)+(b+d)i)；
    (x-y=(a+bi)-(c+di)=(a-c)+(b-d)i)；
    (xy=(a+bi)(c+di)=ac+(bc+ad)i+bdi^2=(ac-bd)+(bc+ad)i)
  复数的三角函数形式：前面说到，复数在复平面上即是一个向量。因此我们可以定义复数(z=a+bi)的模长为(|z|=sqrt{a^2+b^2})，即向量对应的模长；定义复数(z=a+bi)的幅角为向量到实轴正方向的角度为辐角。

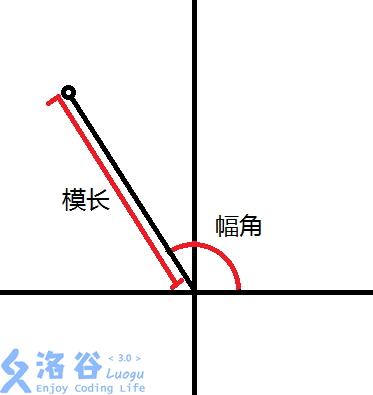
  反过来，我们可以通过模长(|z|)与幅角( heta)来唯一确定一个复数，即(z=|z|(cos heta+isin heta))。
  因此，对于复数(x=|x|(cos heta_x+isin heta_x),y=|y|(cos heta_y+isin heta_y))，复数的乘法也等价于：
  (xy=|x||y|((cos heta_xcos heta_y-sin heta_xsin heta_y)+i(sin heta_xcos heta_y+sin heta_ycos heta_x))=|x||y|(cos( heta_x+ heta_y)+isin( heta_x+ heta_y)))
  即模长相乘，辐角相加。

单位根

  单位根被定义为：方程(x^n=1)在复数域内的所有解。
  莽了？不用担心，我们先聊一聊单位圆。

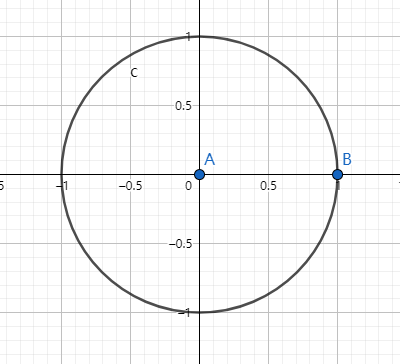
  可以发现，单位圆实际上就是所有的起点在原点且模长为(1)的向量的终点集合。
  另一方面，根据复数运算性质，我们发现，所有解的模长一定是(1)。
  再想一想，解的辐角应该是：(frac{2pi imes 0}{n},frac{2pi imes 1}{n},...,frac{2pi imes (n-1)}n)，只有这些向量自乘(n)次之后，才会落到实轴正半轴上来。
  因此，我们得到了结果：(n)次单位根有(n)个，记为(omega_n^{0sim(n-1)})，其中(omega_n^k)为一个模长为(1)，辐角为(frac{2pi imes k}{n})的复数。
  下图展示了(n=3)时的单位根（们）：

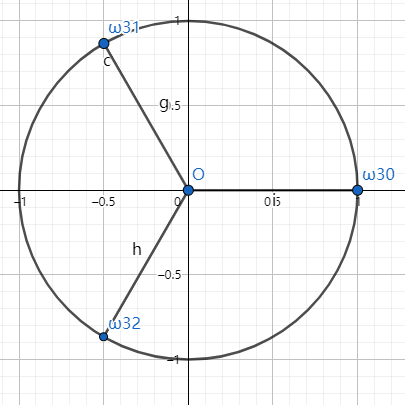
  接下来，有一些关于单位根的重要性质，大家可以按照切蛋糕来理解。
    1.(omega_n^k=(omega_n^1)^k)，证明略；
    2.(omega_n^j imesomega_n^k=omega_n^{j+k})，可用上式证明；
    3.(omega_{2n}^{2k}=omega_n^k)。比如，你一次在蛋糕上切(frac18)，那么你切(4)块就可以得到半块蛋糕；一次切(frac14)，那么你就需要(2)块。
    4.折半引理：当(n)为偶数的时候，(omega_{n}^{(k+frac n2)}=-omega_n^k)。其中(omega_n^{(k+frac n2)}=omega_n^k imesomega_n^{frac n2})，也就是将(omega_n^k)再转半圈之后得到的向量。此时它们模长相等，方向相反，它们就是相反数。

单位根反演

  定理：

[frac1nsum_{k=0}^{n-1}omega_n^{ak}=[n|a] ]

  证明：
  当(n|a)的时候：
    设(a=nt)，原式中所有(omega_n^{ak}=omega_n^{ntk}=omega_n^0=1)，因此原式(=frac1nsum_{k=0}^{n-1}1=1)。
  当(n ot|a)的时候：
    等比数列求和：

[egin{aligned} frac1nsum_{k=0}^{n-1}omega_n^{ak}&=frac1nsum_{k=0}^{n-1}(omega_n^a)^k\ &=frac1n imes frac{1-omega_n^{an}}{1-omega_n^a}\ &=frac1n imes frac{1-1}{1-omega_n^1}\ &=0 end{aligned}]

  于是就证完了。

0.卷积

  卷积是定义在函数上的运算。
  对于函数(f(n))和(g(n))，其卷积((f*g)(n))就是：

[(f*g)(n)=int_{-infty}^{infty}f( au)g(n- au) ext d au ]

  我知道你觉得它很没用，所以这里还有离散的表达：

[(f*g)(n)=sum_{ au=-infty}^{infty}f( au)g(n- au) ]

  你说计算机处理不了实数？好吧，这里还有最后一个，定义在有限序列(f)和(g)上的卷积：

[(f*g)(n)=sum_{i=0}^nf(i)g(n-i) ]

  是不是很熟悉？这就是我们常见的多项式乘法！
  因此，算法竞赛中常常用卷积优化算法 FFT 来进行多项式乘法运算。

1.FFT