题意: 给你一个24格式的数字时间,(字符串),问你这个时刻时针与分针 时针与秒针 分针与秒针 之间的夹角,
我们发现 秒针每秒转6度,分针每秒转1/10度,每分转6度,时针每小时转30度,每分转1/2度,没秒转
1/120 度,那么我们将表盘看做一个坐标系,12点钟为起点,那么可以计算出每个指针这一刻的角度是多少,但是为了避免
分数的加减,我们将所有的数通分,同时乘以120,那么圆盘一圈360 度变成了360*120 =43200度,肯定在int内,将时间转化
为12制的时间,计算角度,然后做差得到角度,但是输出是范围是0-180 ,所以要求小角,选择 min(x,43200-x)作为差值
,然后要化简为最简分式就可以了,(分子是120)
假设当前时间为 H:M:X
时针此时的度数: 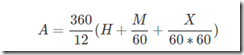
分针此时的度数: 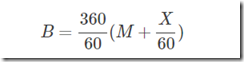
秒针此时的度数: 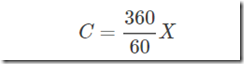
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <stdlib.h>
using namespace std;
int gcd(int a,int b)
{
if(b==0)
return a;
else
return gcd(b,a%b);
}
int main()
{
int h,m,s;
int H,M,S;
int ans1,ans2,ans3;
char str[20];
int t;
cin>>t;
while(t--)
{
cin>>str;
h=(str[0]-'0')*10+(str[1]-'0');
m=(str[3]-'0')*10+(str[4]-'0');
s=(str[6]-'0')*10+(str[7]-'0');
if(h>=12)
h-=12;
//cout<<h<<endl;
H=h*3600+m*60+s;
M=m*720+12*s;
S=s*720;
ans1=max(H,M)-min(H,M);
ans2=max(H,S)-min(H,S);
ans3=max(M,S)-min(M,S);
ans1=min(ans1,43200-ans1);
ans2=min(ans2,43200-ans2);
ans3=min(ans3,43200-ans3);
int g1,g2,g3;
g1=gcd(ans1,120);
g2=gcd(ans2,120);
g3=gcd(ans3,120);
ans1/=g1;
ans2/=g2;
ans3/=g3;
int f1,f2,f3;
f1=120/g1;
f2=120/g2;
f3=120/g3;
if(f1==1)
{
cout<<ans1<<" ";
}
else
{
if(ans1==0)
{
cout<<0<<" ";
}
else
cout<<ans1<<"/"<<f1<<" ";
}
if(f2==1)
{
cout<<ans2<<" ";
}
else
{
if(ans2==0)
cout<<0<<" ";
else
cout<<ans2<<"/"<<f2<<" ";
}
if(f3==1)
{
cout<<ans3<<" "<<endl;
}
else
{
if(ans3==0)
cout<<0<<" "<<endl;
else
cout<<ans3<<"/"<<f3<<" "<<endl;
}
}
return 0;
}