1、问题描述
给定带权有向图G =(V,E),其中每条边的权是非负实数。另外,还给定V中的一个顶点,称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。
2、Dijkstra算法
Dijkstra算法是解单源最短路径问题的贪心算法。
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其他顶点之间的最短路径长度。

伪代码如下:
Dijkstra算法可描述如下,其中输入带权有向图是G=(V,E),V={1,2,…,n},顶点v是源。c是一个二维数组,c[i][j]表示边(i,j)的权。当(i,j)不属于E时,c[i][j]是一个大数。dist[i]表示当前从源到顶点i的最短特殊路径长度。在Dijkstra算法中做贪心选择时,实际上是考虑当S添加u之后,可能出现一条到顶点的新的特殊路,如果这条新特殊路是先经过老的S到达顶点u,然后从u经过一条边直接到达顶点i,则这种路的最短长度是dist[u]+c[u][i]。如果dist[u]+c[u][i]<dist[i],则需要更新dist[i]的值。步骤如下:
(1) 用带权的邻接矩阵c来表示带权有向图, c[i][j]表示弧<vi,vj>上的权值。设S为已知最短路径的终点的集合,它的初始状态为空集。从源点v经过S到图上其余各点vi的当前最短路径长度的初值为:dist[i]=c[v][i], vi属于V.
(2) 选择vu, 使得dist[u]=Min{dist[i] | vi属于V-S},vj就是长度最短的最短路径的终点。令S=S U {u}.
(3) 修改从v到集合V-S上任一顶点vi的当前最短路径长度:如果 dist[u]+c[u][j]< dist[j] 则修改 dist[j]= dist[u]+c[u][j].
(4) 重复操作(2),(3)共n-1次.
算法具体实现如下:

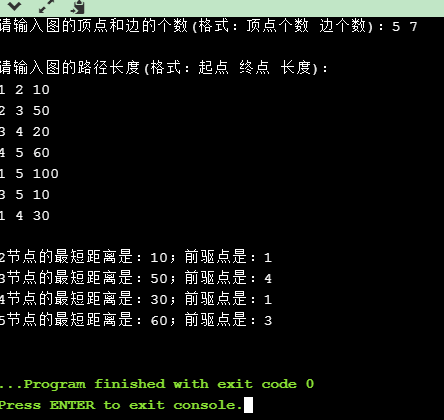
import java.util.Scanner; public class SSSP { public static void main(String[] args) { Scanner input = new Scanner(System.in); System.out.print("请输入图的顶点和边的个数(格式:顶点个数 边个数):"); int n = input.nextInt(); //顶点的个数 int m = input.nextInt(); //边的个数 System.out.println(); int[][] a = new int[n + 1][n + 1]; //初始化邻接矩阵 for(int i = 0; i < a.length; i++) { for(int j = 0; j < a.length; j++) { a[i][j] = -1; //初始化没有边 } } System.out.println("请输入图的路径长度(格式:起点 终点 长度):"); //总共m条边 for(int i = 0; i < m; i++) { //起点,范围1到n int s = input.nextInt(); //终点,范围1到n int e = input.nextInt(); //长度 int l = input.nextInt(); if(s >= 1 && s <= n && e >= 1 && e <= n) { //无向有权图 a[s][e] = l; a[e][s] = l; } } System.out.println(); //距离数组 int[] dist = new int[n+1]; //前驱节点数组 int[] prev = new int[n+1]; int v =1 ;//顶点,从1开始 dijkstra(v, a, dist, prev); } /** * 单源最短路径算法(迪杰斯特拉算法) * @param v 顶点 * @param a 邻接矩阵表示图 * @param dist 从顶点v到每个点的距离 * @param prev 前驱节点数组 */ public static void dijkstra(int v, int[][] a, int[] dist, int[] prev) { int n = dist.length; /** * 顶点从1开始,到n结束,一共n个结点 */ if(v > 0 && v <= n) { //顶点是否放入的标志 boolean[] s = new boolean[n]; //初始化 for(int i = 1; i < n; i++) { //初始化为 v 到 i 的距离 dist[i] = a[v][i]; //初始化顶点未放入 s[i] = false; //v到i无路,i的前驱节点置空 if(dist[i] == -1) { prev[i] = 0; } else { prev[i] = v; } } //v到v的距离是0 dist[v] = 0; //顶点放入 s[v] = true; //共扫描n-2次,v到v自己不用扫 for(int i = 1; i < n - 1; i++) { int temp = Integer.MAX_VALUE; //u为下一个被放入的节点 int u = v; //这个for循环为第二步,观测域为v的观测域 //遍历所有顶点找到下一个距离最短的点 for(int j = 1; j < n; j++) { //j未放入,且v到j有路,且v到当前节点路径更小 if(!s[j] && dist[j] != -1 && dist[j] < temp) { u = j; //temp始终为最小的路径长度 temp = dist[j]; } } //将得到的下一节点放入 s[u] = true; //这个for循环为第三步,用u更新观测域 for(int k = 1; k < n; k++) { if(!s[k] && a[u][k] != -1) { int newdist=dist[u] + a[u][k]; if(newdist < dist[k] || dist[k] == -1) { dist[k] = newdist; prev[k] = u; } } } } } for(int i = 2; i < n; i++) { System.out.println(i + "节点的最短距离是:" + dist[i] + ";前驱点是:" + prev[i]); } } }
例,如图中的有向图,应用 Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程如下表所示:




假设S(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,则有S(i,j)=S(i,k)+S(k,s)+S(s,j)。而S(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径S'(k,s),那么S'(i,j)=S(i,k)+S'(k,s)+S(s,j)<S(i,j)。则与S(i,j)是从i到j的最短路径相矛盾。因此该性质得证。