二项堆

原理参考《算法导论》，仅给出代码。

声明一个mergeable_heap类

class mergeable_heap {//由多棵二项树构成
public:
    typedef struct _HeapNode{
        _HeapNode():key(0), degree(0), p(NULL), c(NULL), sibling(NULL){}
        _HeapNode(int _key, int _degree, _HeapNode *_p, _HeapNode *_c, _HeapNode *_sibling):
            key(_key), degree(_degree), p(_p), c(_c), sibling(_sibling){}
        int key;
        int degree;
        _HeapNode *p, *c, *sibling;//父结点，左子结点，右子结点
    }HeapNode, *pHeapNode;
    typedef struct _Heapinfo {
        _Heapinfo() :H(NULL) {}
        _Heapinfo(HeapNode *_H) :H(_H) {}
        HeapNode *H;
    }Heapinfo, *pHeapinfo;
    mergeable_heap(){
        heapInfo = new Heapinfo();
    }
    ~mergeable_heap() {
        heap_empty();
        delete heapInfo;
        if (_CrtDumpMemoryLeaks())
            printf("内存泄漏，请使用F5 debug模式查看！
");//内存泄漏检测
        else
            printf("无内存泄漏！
");
    }
    HeapNode *heap_min(Heapinfo *pInfo);
    HeapNode *heap_max(Heapinfo *pInfo);
    HeapNode *heap_search(Heapinfo *pInfo, int k);
    HeapNode *heap_union(Heapinfo *pInfo1, Heapinfo *pInfo2);
    HeapNode *heap_merge(Heapinfo *pInfo1, Heapinfo *pInfo2);
    void heap_link(HeapNode *y, HeapNode *z);
    void heap_insert(Heapinfo *pInfo, int k);
    void heap_print(Heapinfo *pInfo);
    Heapinfo *heap_root();//返回引用，解除private属性
    int extract_min();
    int extract_max();
    HeapNode *heap_reverse(HeapNode *H);
    HeapNode *heap_decrease(HeapNode *x, int k);
    HeapNode * heap_increase(HeapNode *x, int k);
    void heap_delete(Heapinfo *pInfo, int k);
    void heap_empty();
private:
    Heapinfo *heapInfo;//包含了所有二项树的根
};

对应成员函数实现

heap_min函数，找出堆中最小结点

typename mergeable_heap::HeapNode *mergeable_heap::heap_min(typename mergeable_heap::Heapinfo *pInfo) {
    HeapNode *x, *y;
    if (pInfo == NULL)
        return NULL;
    x = y = pInfo->H;
    while ((x = x->sibling)) {
        if (x->key < y->key)
            y = x;
    }
    return y;
}

heap_max函数，找出堆中最大结点

typename mergeable_heap::HeapNode *mergeable_heap::heap_max(typename mergeable_heap::Heapinfo *pInfo) {
    HeapNode *x, *y, *z, *H;
    if (pInfo == NULL)
        return NULL;
    z = H = pInfo->H;
    while (H) {
        if (H->key > z->key) z = H;
        x = H->c;
        while (x) {
            //输出同一层的
            y = x;
            while (y) {
                if (y->key > z->key) z = y;
                y = y->sibling;
            }
            x = x->c;
        }
        H = H->sibling;
    }
    return z;
}

heap_search函数，查找对应关键字k的结点

typename mergeable_heap::HeapNode *mergeable_heap::heap_search(typename mergeable_heap::Heapinfo *pInfo, int k) {
    HeapNode *x, *y, *H;
    if (pInfo == NULL)
        return NULL;
    else if (pInfo->H == NULL)
        return NULL;
    H = pInfo->H;
    while (H) {
        if (H->key == k)
            return H;
        x = H->c;
        while (x) {
            //输出同一层的
            y = x;
            while (y) {
                if (y->key == k)
                    return y;
                y = y->sibling;
            }
            x = x->c;
        }
        H = H->sibling;
    }
    return NULL;
}

heap_union函数，两个堆的合并，原理来自于《算法导论》

typename mergeable_heap::HeapNode *mergeable_heap::heap_union(typename mergeable_heap::Heapinfo *pInfo1, typename mergeable_heap::Heapinfo *pInfo2) {
    HeapNode *H = heap_merge(pInfo1, pInfo2);
    HeapNode *prev, *next, *x;
    delete pInfo1;
    delete pInfo2;
    if (H == NULL)
        return NULL;
    prev = NULL;
    x = H;
    next = x->sibling;
    while (next) {
        if (x->degree != next->degree || (next->sibling && next->sibling->degree == x->degree)) {//case 1, 2
            prev = x;
            x = next;
        }
        else if (x->key <= next->key) {//case 3
            x->sibling = next->sibling;
            heap_link(next, x);
        }
        else {//case 4
            if (prev == NULL)
                H = next;
            else
                prev->sibling = next;
            heap_link(x, next);
            x = next;
        }
        next = x->sibling;
    }
    return H;
}

两个对应的辅助函数heap_merge, heap_link

typename mergeable_heap::HeapNode * mergeable_heap::heap_merge(typename mergeable_heap::Heapinfo *pInfo1, typename mergeable_heap::Heapinfo *pInfo2) {
    HeapNode *H = NULL, *x, *r = NULL, *H1 = NULL, *H2 = NULL;
    if (pInfo1 == NULL && pInfo2 == NULL)
        return NULL;
    if (pInfo1) H1 = pInfo1->H;
    if (pInfo2) H2 = pInfo2->H;
    while (H1 || H2) {
        if (H2 == NULL || (H1 && H1->degree <= H2->degree)) {
            x = H1;
            H1 = H1->sibling;
        }
        else {
            x = H2;
            H2 = H2->sibling;
        }
        //插入到H
        if (r)
            r->sibling = x;
        else
            H = x;
        r = x;
    }
    if (r) r->sibling = NULL;
    return H;
}

void mergeable_heap::heap_link(typename mergeable_heap::HeapNode *y, typename mergeable_heap::HeapNode *z) {
    y->p = z;
    y->sibling = z->c;
    z->c = y;
    z->degree = z->degree + 1;
}

heap_insert函数，插入关键字到堆

void mergeable_heap::heap_insert(typename mergeable_heap::Heapinfo *pInfo, int k) {
    HeapNode *x;
    Heapinfo *pNew;
    if (heap_search(pInfo, k)) //不允许重复插入
        return;
    x = new HeapNode();
    x->key = k;
    pNew = new Heapinfo(x);
    if (pInfo == heapInfo)
        heapInfo = new Heapinfo(heap_union(pInfo, pNew));
    else {
        pNew = new Heapinfo(heap_union(pInfo, pNew));
        heapInfo = new Heapinfo(heap_union(heapInfo, pNew));
    }
}

extract_min函数，提取最小结点，并删除之

int mergeable_heap::extract_min() {
    HeapNode *x, *y;
    int k;
    Heapinfo *pNew = NULL;
    if (heapInfo == NULL)
        return -1;
    x = y = heapInfo->H;
    k = heapInfo->H->key;
    while (x->sibling) {//找到最小y的前一个结点
        if (x->sibling->key < y->key) {
            y = x;//y是最小结点的前一个结点
            k = y->sibling->key;
        }
        x = x->sibling;
    }
    x = y;//前一个结点
    if (y->sibling && y->sibling->key == k)
        y = y->sibling;//当前最小结点
    if (x == y) {//剔除x，修复连接
        x = x->sibling;
        heapInfo->H = x;
    }
    else
        x->sibling = x->sibling->sibling;
    x = y->c;
    while (x) {//清理父结点
        x->p = NULL;
        x = x->sibling;
    }
    x = heap_reverse(y->c);
    pNew = new Heapinfo(x);
    heapInfo = new Heapinfo(heap_union(heapInfo, pNew));
    delete y;
    return k;
}

extract_max函数，提取最大结点，并删除之

int mergeable_heap::extract_max() {
    HeapNode *x = heap_max(heapInfo);
    int k = x->key;
    heap_delete(heapInfo, k);
    return k;
}

heap_decrease函数，下降关键字

typename mergeable_heap::HeapNode *mergeable_heap::heap_decrease(typename mergeable_heap::HeapNode *x, int k) {
    HeapNode *y, *z;
    if (k >= x->key)
        return NULL;
    x->key = k;
    y = x;
    z = x->p;
    while (z && y->key < z->key) {
        std::swap(y->key, z->key);
        y = z;
        z = y->p;
    }
    return y;
}

heap_increase函数，提升关键字

typename mergeable_heap::HeapNode *mergeable_heap::heap_increase(typename mergeable_heap::HeapNode *x, int k) {
    HeapNode *y, *z;
    if (k <= x->key)
        return NULL;
    x->key = k;
    y = x;
    z = x->c;
    while (z && y->key > z->key) {
        std::swap(y->key, z->key);
        y = z;
        z = y->c;
    }
    return y;
}

heap_delete函数，堆思想删除，类似Treap树的删除原理

void mergeable_heap::heap_delete(typename mergeable_heap::Heapinfo *pInfo, int k) {
    //堆删除思想，原理由heap_decrease和extract_min构成
    HeapNode *x, *y, *z;
    Heapinfo *pNew = NULL;
    x = heap_search(pInfo, k);
    if (x == NULL)
        return;
    y = x;
    z = x->p;
    while (z) {//需要删除的结点上升到根
        std::swap(y->key, z->key);
        y = z;
        z = y->p;
    }
    //定位p结点的前一个结点
    x = y;//保留当前结点
    y = z = pInfo->H;
    while (z != x) {
        y = z;//前驱
        z = z->sibling;
    }
    x = y;//前一个结点
    if (y->sibling && y->sibling->key == k)
        y = y->sibling;//当前最小结点
    if (x == y) {//剔除x，修复连接
        x = x->sibling;
        pInfo->H = x;
    }
    else
        x->sibling = x->sibling->sibling;
    x = y->c;
    while (x) {//清理父结点
        x->p = NULL;
        x = x->sibling;
    }
    x = heap_reverse(y->c);
    pNew = new Heapinfo(x);
    if (pInfo == heapInfo)
        heapInfo = new Heapinfo(heap_union(pInfo, pNew));
    else {
        pNew = new Heapinfo(heap_union(pInfo, pNew));
        heapInfo = new Heapinfo(heap_union(heapInfo, pNew));
    }
    delete y;
}

对应的辅助函数heap_reverse，让指定堆倒序

typename mergeable_heap::HeapNode *mergeable_heap::heap_reverse(typename mergeable_heap::HeapNode *H) {
    HeapNode *x = NULL, *y;
    if (H == NULL)
        return NULL;
    while (H) {//H变为逆序
        y = H->sibling;
        if (x == NULL) 
            H->sibling = NULL;
        else 
            H->sibling = x;
        x = H;
        H = y;
    }
    return x;
}

heap_empty函数，清理堆

void mergeable_heap::heap_empty() {
    while (heapInfo && heapInfo->H) {
        heap_delete(heapInfo, heapInfo->H->key);
        heap_print(heapInfo);
        printf("
");
    }
}

heap_print和heap_root函数

void mergeable_heap::heap_print(typename mergeable_heap::Heapinfo *pInfo) {
    HeapNode *x, *y, *H;
    if (pInfo == NULL)
        return;
    H = pInfo->H;
    while (H) {
        printf("[B%d]%d
", H->degree, H->key);
        x = H->c;
        while (x) {
            //输出同一层的
            y = x;
            while (y) {
                printf("%d, df=%d %-02s", y->key, y->degree, " ");
                y = y->sibling;
            }
            printf("
");
            x = x->c;
        }
        H = H->sibling;
    }
}

typename mergeable_heap::Heapinfo *mergeable_heap::heap_root() {
    return heapInfo;
}

数据测试

        int K[] = { 10,1,12,18,25,6,8,14,29,11,17,38,27 };

Main函数

int main()
{
    //int K[] = { 12,7,25,15,28,33,41 };
    int K[] = { 10,1,12,18,25,6,8,14,29,11,17,38,27 };
    mergeable_heap heap;
    for (int i = 0; i < LENGTH(K); i++)
        heap.heap_insert(heap.heap_root(), K[i]);
    heap.heap_print(heap.heap_root());
    printf("
");
    /*
    //测试heap_delete函数
    printf("测试heap_delete函数...
");
    //for (int i = LENGTH(K) - 1; i >= 0; i--) {
    for (int i = 0; i < LENGTH(K); i++) {
        printf("%d deleted
", K[i]);
        heap.heap_delete(heap.heap_root(), K[i]);
        heap.heap_print(heap.heap_root());
        printf("
");
    }
    */
    printf("对象释放...
");
    return 0;
}

结果图

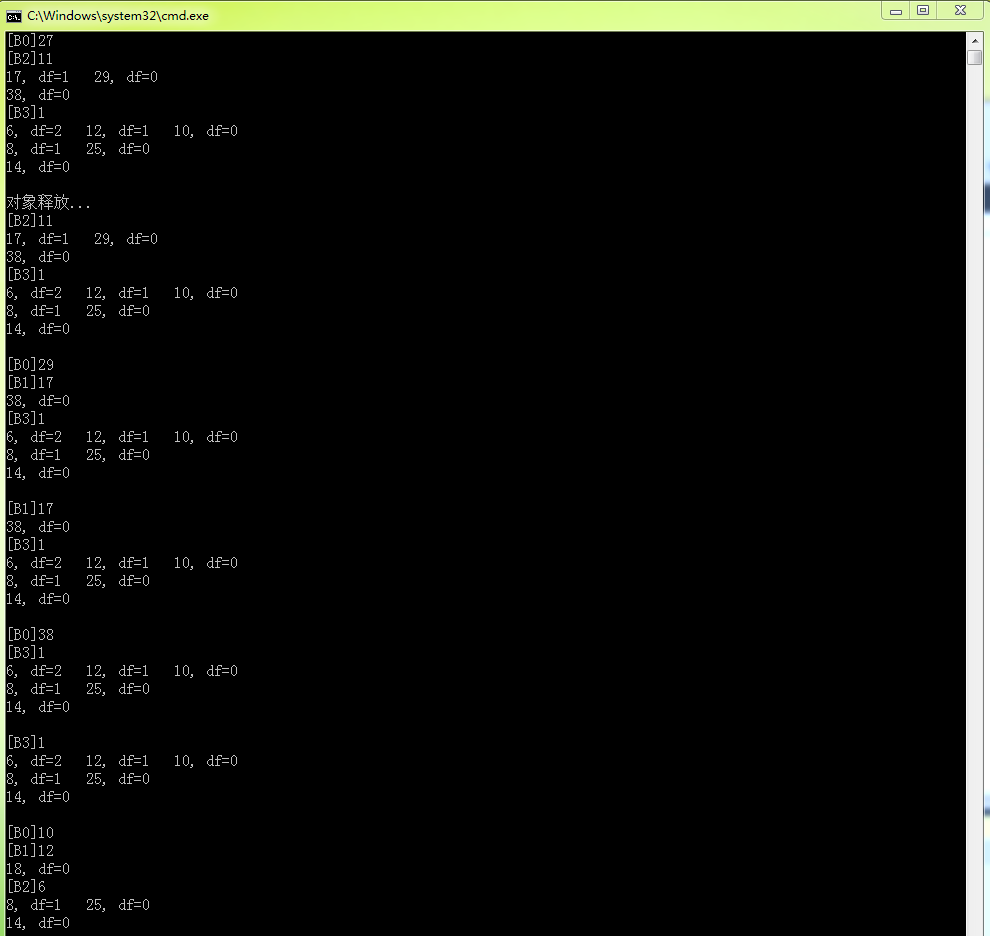
代码均经过测试，结果正确！！！