3. 快速排序

　　快速排序（Quick Sort）与冒泡排序均为交换类排序。快排是对冒泡排序的一种改进。由于关键字的比较和交换是跳跃进行的，因此，快速排序是一种不稳定的排序方法。

 

0. 序

1. 冒泡排序

2. 快速排序

2.1 基本思想

2.2 一趟快速排序（一趟划分）

2.3 过程

2.4 实现

2.5 复杂度分析

2.5.1 时间复杂度（包含证明）

2.5.2 空间复杂度

       0. 序

　　快速排序算法最早由图灵奖获得者Tony Hoare设计出来的，他在形式化方法理论以及ALGOL60编程语言的发明中都有卓越的贡献，是上世纪最伟大的计算机科学家之一。

　　快速排序被列为20世纪十大算法之一。

　　1. 冒泡排序

　　假设在排序过程中，记录序列R[1...n] 的状态为：

 

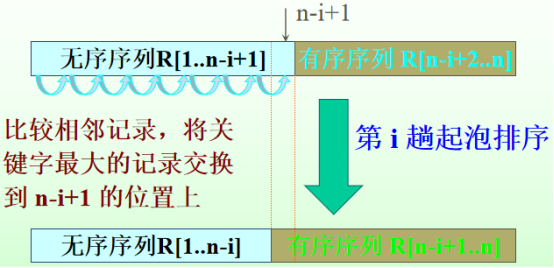
　　更多的冒泡排序讲解见https://www.cnblogs.com/datamining-bio/p/9715774.html

　　2. 快速排序

　　快速排序也是通过不断比较和移动交换来实现排序的，只不过它的实现，增大了记录的比较和移动的距离，将关键字较大的记录从前面直接移动到后面，关键字较小的记录从后面直接移动到前面，从而减少了总的比较次数和移动交换次数。

　　2.1 基本思想

　　通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，然后分别对这两部分继续进行排序，直到整个序列有序。

　　2.2 一趟快速排序（一次划分）

　　目标：找一个记录，以它的关键字作为“枢纽”，凡其关键字小于枢纽的记录均移动至该记录之前，反之，凡关键字大于枢纽的记录均移动至该记录之后。

 

 

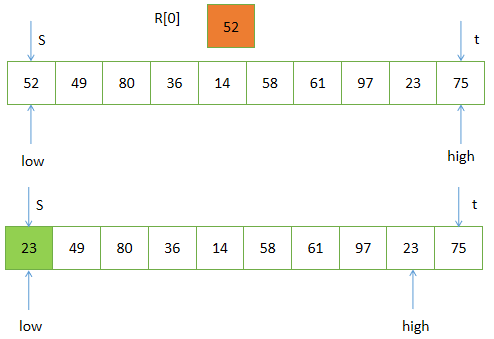
　　设 R[s] = 52 为枢纽

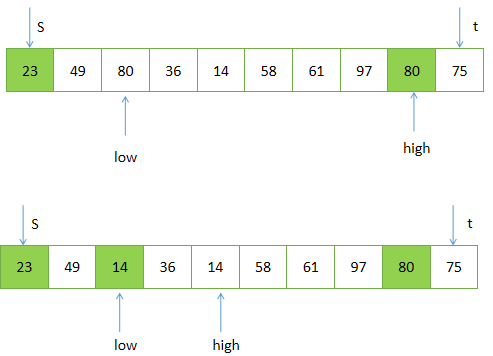
　　将R[high].key 和枢纽的关键字进行比较，要求R[high].key ≥ 枢纽的关键字

　　将R[low].key 和枢纽的关键字进行比价，要求R[low].key ≤ 枢纽的关键字

 

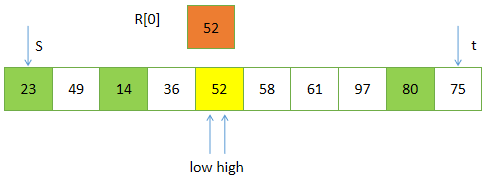
　　可见，经过“一次划分”，将关键字序列：

　　52,  49， 80， 36， 14， 58， 61， 97， 23， 75

　　调整为： 23， 49， 14， 36， （52），58,  61，97,  80， 75

　　在调整过程中，设立了两个指针：low 和 high，它们的初值分别为：s 和 t 

　　之后逐渐减小high，增加low，并保证 R[high].key ≥ 52，和 R[low].key ≤ 52，否则进行记录的“交换”。

　　2.3 过程

　　首先对无序的记录序列进行“一次划分”，之后分别对分割所得两个子序列“递归”进行快速排序。

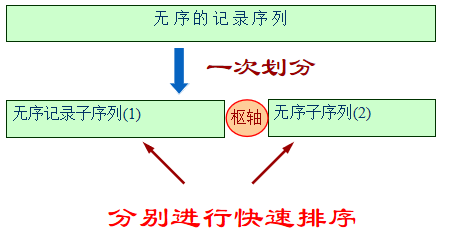
 　　2.4 实现

// 快速排序  O(nlogn) --->逆序O(n^2)
// 调用QSort(1, n)   待排记录index = 1 ... n
public int[] QSort(int low, int high){
    if(low < high){
        int p = Partition(low, high);
        QSort(low, p-1);
        QSort(p+1, high);
    }
    return needSort;
}
private int Partition(int low, int high){
    needSort[0] = needSort[low];
    while(low < high){
        while(low < high && needSort[high] >= needSort[0]) high--;
        needSort[low] = needSort[high];
        while(low < high && needSort[low] <= needSort[0]) low++;
        needSort[high] = needSort[low];
    }
    needSort[low] = needSort[0];
    return low;
}

　　2.5  复杂度分析

　　2.5.1 时间复杂度

　　① 在最优情况下，Partition每次都划分得很均匀，如果排序n个关键字，其递归树（见2.5.2）的深度就为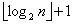，即仅需递归log₂n次，需要时间为T(n)的话，第一次Partition应该是需要对整个数组扫描一遍，做n次比较。然后，获得的枢纽将数组一分为二，那么各自还需要T(n/2)的时间（注意是最好情况，所以平分两半）。于是不断地划分下去，我们就有了下面的不等式推断。　

T(n) ≤ 2T(n/2) + n, T(1) = 0

T(n) ≤ 2( 2T(n/4) + n/2 ) + n = 4T(n/4) + 2n

T(n) ≤ 4( 2T(n/8) + n/4 ) + 2n = 8T(n/8) + 3n

...

T(n) ≤ nT(1) + (log₂n) * n = O(nlogn)

　　

　　不知道为什么是“≤”而不是“＝”？ 待补充

　　也就是说，在最优的情况下，快速排序算法的时间复杂度为O(nlogn)。

　　② 在最坏情况下，待排序的序列为正序或逆序，每次划分只得到一个比上一次划分少一个记录的子序列，注意另一个为空。如果递归树画出来，它是一颗斜树。此时需要执行n-1次递归调用，且第i次划分需要经过n-i次关键字的比较才能找到第i个记录，也就是枢纽的位置，因此比较次数为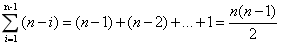，最终其时间复杂度为O(n²)。

　　③ 平均的情况，设枢纽的关键字应该在第k的位置（1≤k≤n），每个位置的概率相同，均为1/n，那么：

 

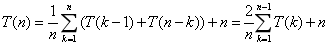
　　数学归纳法可证明，其数量级为O(nlogn)。 待补充

　　通常，快速排序被认为是在所有同数量级O(nlogn) 的排序方法中，其平均性能是最好的。但是，若待排记录的初始状态为按关键字有序或基本有序时，快速排序将蜕化为冒泡排序，其时间复杂度为O(n²)。

　　为避免出现这种情况，需在进行一次划分之前，进行“预处理”，即：先对R(s),key， R(t).key和 R[└(s+t)/2┘].key，进行相互比较，然后取关键字为“三者之中”的记录为枢纽记录。

　　2.5.2 空间效率

　　举例：

 

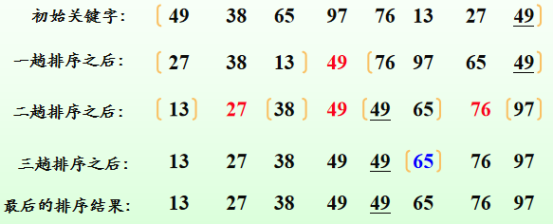
　　快速排序的递归过程可用生成一颗二叉树形象地给出，下图对应上面例子递归调用过程的二叉树。

 

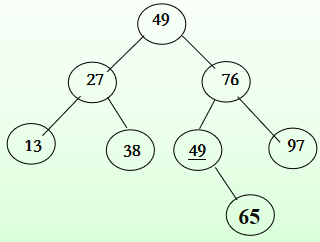
　　快速排序是递归的，每层递归调用时的指针和参数均要用栈来存放，递归调用层数与上述二叉树的深度一致。因而，存储开销在理想情况下为O(log₂n)，即树的高度，其空间复杂度也就为O(logn)；在最坏情况下，需要进行n-1次递归调用，即二叉树是一个单链，为O(n)；平均情况，空间复杂度也为O(logn)。

　　注意，由于关键字的比较和交换是跳跃进行的，因此，快速排序是一种不稳定的排序方法。

参考：

　　上课ppt

　　《大话数据结构》程杰著  清华大学出版社，2011.6（2017.6 重印）