数论练习

欧拉函数：

 

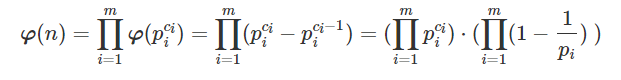
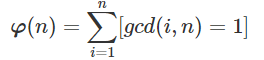
 欧拉函数筛法：

const int N = 5e6 + 5;

ull ans[N];
void count(int n)        //求1~maxv的所有欧拉函数
{
    memset(ans, 0, sizeof(ans));
    for (int i = 2; i < n; i++) {
        if (!ans[i])    //第一个ans[i] == 0 的都是素数
        {
            for (int j = i; j < n; j += i)    //素数的倍数
            {
                if (!ans[j])
                    ans[j] = j;    //对素数倍数赋值
                ans[j] = ans[j] / i * (i - 1);    //求欧拉函数的值
            }
        }
    }
    for (int i = 2; i < n; i++)
        ans[i] = ans[i - 1] + ans[i];
}

1007:

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <sstream>
#include <cstdio>
#include <cstring>
#include <numeric>
#include <cmath>
#include <iomanip>
#include <deque>
#include <bitset>
#include <cassert>
#include <unordered_set>
#include <unordered_map>
#define ll              long long
#define ull             unsigned long long
#define pii             pair<int, int>
#define pll             pair<ll,ll>                 
#define rep(i,a,b)      for(int  i=a;i<=b;i++)
#define dec(i,a,b)      for(int  i=a;i>=b;i--)
#define forn(i, n)      for(int i = 0; i < int(n); i++)
using namespace std;
int dir[4][2] = { { 1,0 },{ 0,1 } ,{ 0,-1 },{ -1,0 } };
const long long INF = 0x7f7f7f7f7f7f7f7f;
const int inf = 0x3f3f3f3f;
const double pi = acos(-1.0);
const double eps = 1e-6;

inline ll read()
{
    ll x = 0; bool f = true; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = false; c = getchar(); }
    while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    return f ? x : -x;
}

ll gcd(ll m, ll n)
{
    return n == 0 ? m : gcd(n, m % n);
}

ll qpow(ll m, ll k, ll mod)
{
    ll res = 1, t = m;
    while (k)
    {
        if (k & 1)
            res = res * t % mod;
        t = t * t % mod;
        k >>= 1;
    }
    return res;
}
/**********************************************************/

const ll mod = 1e9 + 7;
const int N = 5e6 + 5;

ull ans[N];
void count(int n)        //求1~maxv的所有欧拉函数
{
    memset(ans, 0, sizeof(ans));
    for (int i = 2; i < n; i++) {
        if (!ans[i])    //第一个ans[i] == 0 的都是素数
        {
            for (int j = i; j < n; j += i)    //素数的倍数
            {
                if (!ans[j])
                    ans[j] = j;    //对素数倍数赋值
                ans[j] = ans[j] / i * (i - 1);    //求欧拉函数的值
            }
        }
    }
    for (int i = 2; i < n; i++)    //求平方和
        ans[i] = ans[i - 1] + ans[i] * ans[i];
}

int main()
{
#ifdef _DEBUG
    freopen("input.txt", "r", stdin);
    freopen("output.txt", "w", stdout);
#endif
    count(N);
    int T;
    cin >> T;
    rep(i,1,T)
    {
        int a, b;
        cin >> a >> b;
        printf("Case %d: %llu
", i, ans[b] - ans[a - 1]);
    }
}