我们之前接触的所有机器学习算法都有一个共同特点,那就是分类器会接受2个向量:一个是训练样本的特征向量X,一个是样本实际所属的类型向量Y。由于训练数据必须指定其真实分类结果,因此这种机器学习统称为有监督学习。
然而有时候,我们只有训练样本的特征,而对其类型一无所知。这种情况,我们只能让算法尝试在训练数据中寻找其内部的结构,试图将其类别挖掘出来。这种方式叫做无监督学习。由于这种方式通常是将样本中相似的样本聚集在一起,所以又叫聚类算法。
下面我们介绍一个最常用的聚类算法:K均值聚类算法(K-Means)。
1、K均值聚类
K-Means算法思想简单,效果却很好,是最有名的聚类算法。聚类算法的步骤如下:
1:初始化K个样本作为初始聚类中心;
2:计算每个样本点到K个中心的距离,选择最近的中心作为其分类,直到所有样本点分类完毕;
3:分别计算K个类中所有样本的质心,作为新的中心点,完成一轮迭代。
通常的迭代结束条件为新的质心与之前的质心偏移值小于一个给定阈值。
下面给一个简单的例子来加深理解。如下图有4个样本点,坐标分别为A(-1,-1),B(1,-1),C(-1,1),D(1,1)。现在要将他们聚成2类,指定A、B作为初始聚类中心(聚类中心A0, B0),指定阈值0.1。K-Means迭代过程如下:
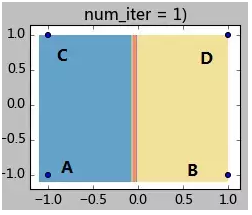
step 1.1:计算各样本距离聚类中心的距离:
样本A:d(A,A0) = 0; d(A,B0) = 2;因此样本A属于A0所在类;
样本B:d(B,A0) = 2; d(B,B0) = 0;因此样本B属于B0所在类;
样本C:d(C,A0) = 2; d(C,B0) = 2.8;;因此样本C属于A0所在类;
样本C:d(D,A0) = 2.8; d(D,B0) = 2;;因此样本C属于B0所在类;
step 1.2:全部样本分类完毕,现在计算A0类(包含样本AC)和B0类(包含样本BD)的新的聚类中心:
A1 = (-1, 0); B1 = (1,0);
step 1.3:计算聚类中心的偏移值是否满足终止条件:
|A1-A0| = |(-1,0)-(-1,-1) | = |(0,1)| = 1 >0.1,因此继续迭代。
此时的状态如下图所示:
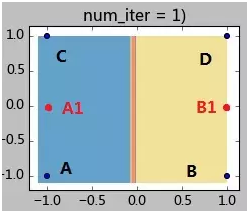
step 2.1:计算各样本距离聚类中心的距离:
样本A:d(A,A1) = 1; d(A,B1) = 2.2;因此样本A属于A1所在类;
样本B:d(B,A1) = 2.2; d(B,B1) = 1;因此样本B属于B1所在类;
样本C:d(C,A1) = 1; d(C,B1) = 2.2;;因此样本C属于A1所在类;
样本D:d(D,A1) = 2.2; d(D,B1) = 1;;因此样本C属于B1所在类;
step 2.2:全部样本分类完毕,现在计算A1类(包含样本AC)和B1类(包含样本BD)的新的聚类中心:
A2 = (-1, 0); B2 = (1,0);
step 2.3:计算聚类中心的偏移值是否满足终止条件:
|A2-A1| = |B2-B1| = 0 <0.1,因此迭代终止。
2、测试数据
下面这个测试数据有点类似SNS中的好友关系,假设是10个来自2个不同的圈子的同学的SNS聊天记录。显然,同一个圈子内的同学会有更密切的关系和互动。
数据如下所示,每一行代表一个好友关系。如第一行表示同学0与同学1的亲密程度为9(越高表示联系越密切)。
显然,这个数据中并没有告知我们这10个同学分别属于哪个圈子。因此我们的目标是使用K-Means聚类算法,将他们聚成2类。
[plain] view plaincopy
- 0 1 9
- 0 2 5
- 0 3 6
- 0 4 3
- 1 2 8
- ......
这个例子设计的很简单。我们使用上一篇文章中提到的关系矩阵,将其可视化出来,会看到如下结果:
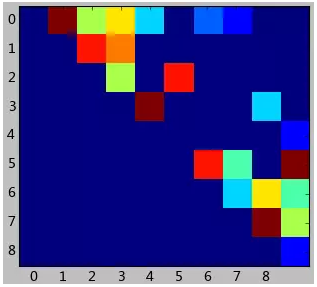
这是个上三角矩阵,因为这个数据中认为好友关系是对称的。上图其实很快能发现,0,1,2,3,4用户紧密联系在一起,而5,6,7,8,9组成了另外一个圈子。
下面我们看看K-Means算法能否找出这个答案。
3、代码与分析
K-Means算法的Python代码如下:
[python] view plaincopy
- # -*- coding: utf-8 -*-
- from matplotlib import pyplot
- import scipy as sp
- import numpy as np
- from sklearn import svm
- import matplotlib.pyplot as plt
- from sklearn.cluster import KMeans
- from scipy import sparse
- #数据读入
- data = np.loadtxt('2.txt')
- x_p = data[:, :2] # 取前2列
- y_p = data[:, 2] # 取前2列
- x = (sparse.csc_matrix((data[:,2], x_p.T)).astype(float))[:, :].todense()
- nUser = x.shape[0]
- #可视化矩阵
- pyplot.imshow(x, interpolation='nearest')
- pyplot.xlabel('用户')
- pyplot.ylabel('用户')
- pyplot.xticks(range(nUser))
- pyplot.yticks(range(nUser))
- pyplot.show()
- #使用默认的K-Means算法
- num_clusters = 2
- clf = KMeans(n_clusters=num_clusters, n_init=1, verbose=1)
- clf.fit(x)
- print(clf.labels_)
- #指定用户0与用户5作为初始化聚类中心
- init = np.vstack([ x[0], x[5] ])
- clf = KMeans(n_clusters=2, init=init)
- clf.fit(x)
- print(clf.labels_)
输出结果如下:
Initialization
complete
Iteration 0, inertia 581.000
Iteration 1, inertia 417.643
Converged at iteration 1
[0 0 1 1 1 1 1 1 1]
[0 0 0 0 1 1 1 1 1]
可以看到,使用默认的K-Means算法将使用随机的初始值,因此每次执行的结果都不一样。
上面的输出中将0,1用户聚类到一起,效果并不理想。然而,如果我们可以确定用户0与用户5是有很大区别的,就可以指定用户0和用户5作为K-Means聚类算法的初始值。可以看到和我们的预期完全一致,这样效果就非常好了。