matlab求单峰函数最小值

测试函数是-x*sin(x)，求其在0~4.5上的最小值。

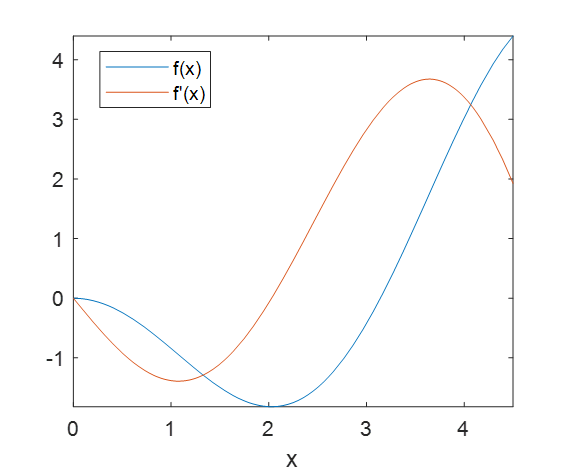
首先绘图观察一下：

fplot(@(x) -x*sin(x),[0,4.5]);
hold on;
fplot(@(x) -sin(x)-x*cos(x),[0,4.5]);
hold off;
legend('f(x)',"f'(x)");
xlabel('x');

[x,fval] = fmincon(@(x) -x*sin(x),2)

x =
2.028757520194786
fval =
-1.819705741159516

可以看到x在2附近f(x)取到最小值。

三点二次插值

下面构建三点二次插值函数：

function [p1,fval]=int2p3(f,xinterval)
p0=xinterval(1);
p2=xinterval(2);
p1=(p0+p2)/2;
while true
    x=[p0,p1,p2];
    y=[f(p0),f(p1),f(p2)];
    c=polyfit(x,y,2);
    p1_=-c(2)/2/c(1);
    if f(p1)<f(p1_)
        if p1<p1_
            p2=p1_;
        else
            p0=p1_;
        end
    else
        if p1<p1_
            p0=p1;
            p1=p1_;
        else
            p2=p1;
            p1=p1_;
        end
    end
    if p2-p0<0.001
        fval=f(p1);
        break
    end
end
end

测试：

>> [x,fval]=int2p3(@(x) -x*sin(x),[0,4.5])
x =
2.028757824672632
fval =
-1.819705741159653

点x的迭代过程如下图：

最后收敛到2.029。

牛顿法

function [p1,fval]=newton(f,xinterval)
p0=xinterval(1);
p2=xinterval(2);
p1=(p0+p2)/2;
d=0.001;
while true
    p1_=(f(p1+d)-f(p1))/d;%一阶导数
    p1_2=(f(p1)-f(p1-d))/d;
    p1__=(p1_-p1_2)/d;%二阶导数
    p1next=p1-p1_/p1__;
    if abs(p1next-p1)<d
        fval=f(p1);
        break
    else
        p1=p1next;
    end
end
end

>> [x,fval]=newton(@(x) -x*sin(x),[0,4.5])
x =
2.028286879504392
fval =
-1.819705441320462