介绍
作者:dragonbean
从名字solutions就能看出,这个py文件是一个算法集,内涵了多种不同的solution算法,下面就来对其中的算法进行讲解。算法所处理的对象是 visual.py 传来的可视点的字典。
{障碍物顶点:[可视点,可视点,可视点,...],...} 数据结构是:{(x0,y0):[(x1,y1),(x3,y3),...],(x1,y1):[(x0,y0),...],...}
算法一
全部递归 全局最优
对某个点的所有可视点进行遍历,遍历时又对遍历到的点的所有可视点进行遍历(简单说就是递归),直到被遍历到的点是终止点,就返回到上层递归里去。
'''
author:dragonbean
href:https://www.cnblogs.com/dragonbean/p/13498421.html
blog:https://www.cnblogs.com/dragonbean/
'''
def solution_one(start, end, graph):
def __searchPath(start, end, graph):
results = []
__generatePath(graph, [start,0], end, results)
results.sort(key=lambda x:x[-1])
return results
def __generatePath(graph, path, end, results):
current = path[-2]
if current == end:
results.append(path)
#print(path)
else:
for n in graph[current]:
if n not in path and path[-1]<(minDistance*1.5): #递归深度为 3/2起始点终止点间距离
distance = path[-1] + math.sqrt((n[0]-path[-2][0])**2 + (n[1]-path[-2][1])**2) #增量计算不同路径的距离
__generatePath(graph, path[:-1]+[n,distance], end, results)
def showPath(results):
print('The path from ', results[0][0], 'to' , results[0][-1], 'is :')
for path in results:
print(path)
minDistance = math.sqrt((end[1]-start[1])**2 + (end[0]-start[0])**2)
results = __searchPath(start, end, graph)
if __name__ == "__main__":
showPath(results)
return results[0]
这里需要注意的是,我对递归的深度做了优化处理,导致递归量大幅减小:在递归的过程中记录路程长度,并与起始点、终止点间距离的1.5倍做比较,小于这个数值的将继续递归下去,大于的将直接返回递归。这么处理可以有效避免多余的内存开销,只是这个1.5倍不对所有情况适用,属于这里的bug。
算法二
直接寻路 局部最优
从起始点开始,遍历该点的所有可视点,计算到该可视点的直线距离与该可视点到终止点的直线距离之和,比较后得出最优的可视点,作为下一次递归的“起始点”,一步一步直到找到终止点end。
'''
author:dragonbean
href:https://www.cnblogs.com/dragonbean/p/13498421.html
blog:https://www.cnblogs.com/dragonbean/
'''
def solution_two(start, end, graph):
print(graph)
#还阔以再优化,再计算多一个点,就更趋于最优了
def __findNext(start,end,graph, path):
minDistance = [None,None]
for each in graph[start]:
if each == end:
path.append(end)
return
else:
distance = math.sqrt((each[0]-start[0])**2+(each[1]-start[1])**2)+math.sqrt((end[0]-each[0])**2+(end[1]-each[1])**2)
if minDistance[1]==None or minDistance[1]>distance:
minDistance = [each,distance]
print(minDistance[0])
path.append(minDistance[0])
__findNext(minDistance[0],end, graph, path)
path = [start]
__findNext(start, end, graph, path)
print(path)
return path
还可以对这个算法进行优化,正如注释里所说的,多计算一层的点(就是可视点的下一层所有可视点的“距离”也计算在内进行比较),以选出最优的第一个可视点,接着对它进行递归。
'''
author:dragonbean
href:https://www.cnblogs.com/dragonbean/p/13498421.html
blog:https://www.cnblogs.com/dragonbean/
'''
def solution_three(start, end, graph):
def __findNext(start,end,graph, path):
minDistance = [None,None]
for each in graph[start]:
if each in path:
continue
elif each == end:
path.append(end)
return
next_min_distance = None
tmp_list = graph[each][:]
try:
tmp_list.remove(start)
print(start)
print(tmp_list)
except:
pass
for i in tmp_list:
if i == end:
path.extend([each,i])
return
next_distance = math.sqrt((end[0]-i[0])**2+(end[1]-i[1])**2) + math.sqrt((i[0]-each[0])**2+(i[1]-each[1])**2)
if next_min_distance==None or next_min_distance>next_distance:
next_min_distance = next_distance
distance = next_min_distance + math.sqrt((each[0]-start[0])**2+(each[1]-start[1])**2)
if minDistance[1]==None or minDistance[1]>distance:
minDistance = [each,distance]
path.append(minDistance[0])
__findNext(minDistance[0],end, graph, path)
path = [start]
__findNext(start, end, graph, path)
print(path)
return path
还有一种优化,是将算法一和算法二结合起来,先确定一条可行的路径,将这个可行路径的值作为算法一递归深度的阈值,对算法一的全局最优做优化。
'''
author:dragonbean
href:https://www.cnblogs.com/dragonbean/p/13498421.html
blog:https://www.cnblogs.com/dragonbean/
'''
def solution_four(start, end, graph):
def __searchPath(start, end, graph):
results = []
__generatePath(graph, [start,0], end, results)
results.sort(key=lambda x:x[-1])
return results
def __generatePath(graph, path, end, results):
current = path[-2]
if current == end:
results.append(path)
#print(path)
else:
for n in graph[current]:
if n not in path and path[-1]<(minDistance*1.5):
distance = path[-1] + math.sqrt((n[0]-path[-2][0])**2 + (n[1]-path[-2][1])**2) #增量计算不同路径的距离
__generatePath(graph, path[:-1]+[n,distance], end, results)
def showPath(results):
print('The path from ', results[0][0], 'to' , results[0][-1], 'is :')
for path in results:
print(path)
#先得到一条可行的路径,将它的长度作为阈值。
prePath = solution_three(start,end,graph)
minDistance = 0.0
for i in range(len(prePath)-1):
minDistance += math.sqrt((prePath[i+1][0]-prePath[i][0])**2+(prePath[i+1][1]-prePath[i][1])**2)
results = __searchPath(start, end, graph)
return results[0]
SPFA算法
队列优化算法
基于spfa(Shortest Path Faster Algorithm)算法思想编写,确实是路程最短、耗时最少的算法(就我之前写的这些算法而言)。可真是太棒了这个算法。至于这个算法本身我就不过多的赘述,可自行百度哦。
解释不下去了,我还是讲一下spfa
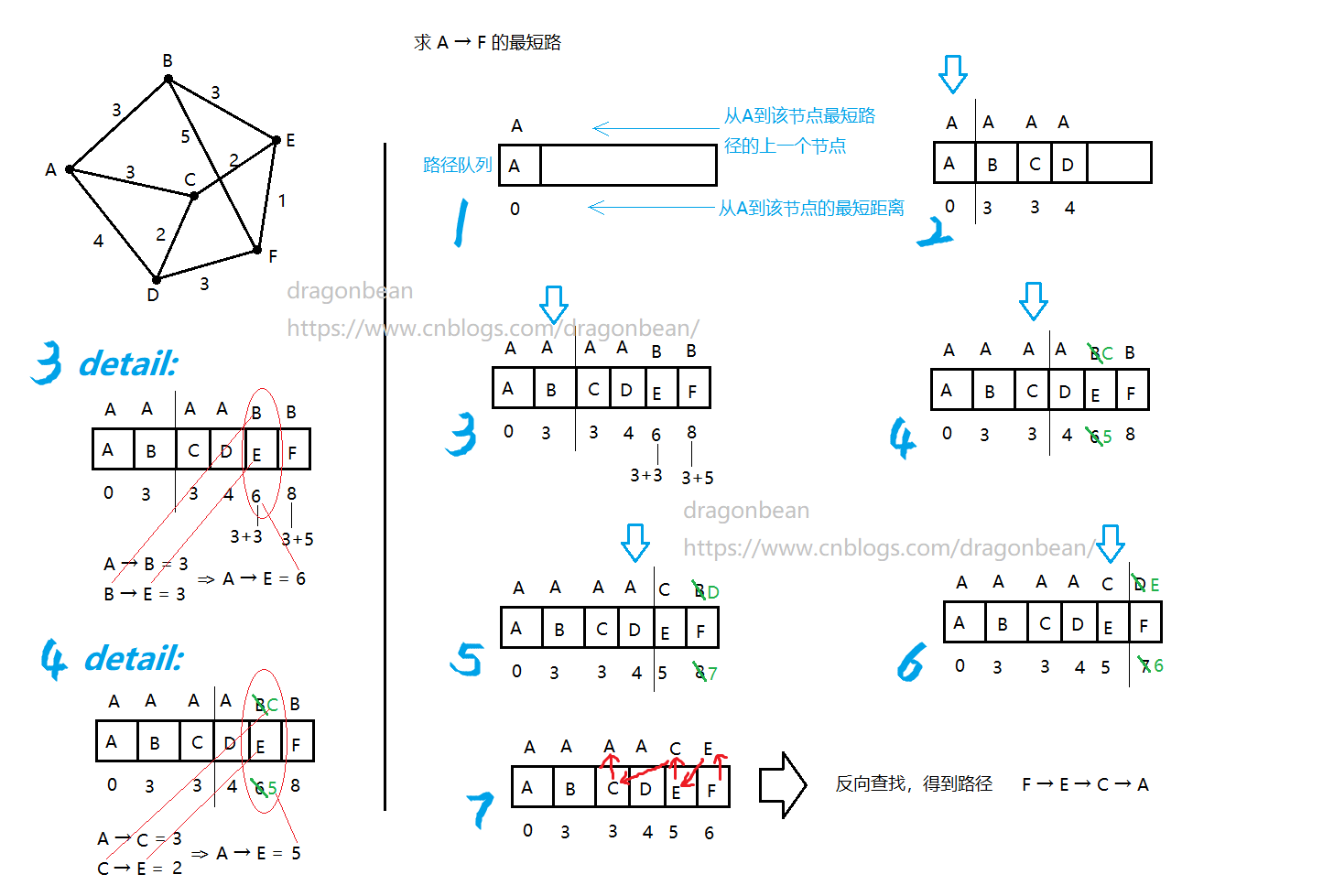
'''
author:dragonbean
href:https://www.cnblogs.com/dragonbean/p/13498421.html
blog:https://www.cnblogs.com/dragonbean/
'''
def solution_spfa(start, end, graph):
#核心代码
def spfa(point):
visualpoint = graph[point]
#如果这个点可以直接可视终止点end,那么这个点到end点的距离一定是最短的,两点之间直线最短。
if end in visualpoint:
distance = math.sqrt((point[0]-end[0])**2 + (point[1]-end[1])**2)
distance += roadDict[point][1]
if roadDict.get(end):
oldDistance = roadDict[end][1]
if distance < oldDistance:
roadDict[end] = [point,distance]
else:
roadList.append(end)
roadDict[end] = [point,distance]
else:
#一般情况处理【核心】
for each in visualpoint:
distance = math.sqrt((point[0]-each[0])**2 + (point[1]-each[1])**2)
distance += roadDict[point][1]
if roadDict.get(each):
oldDistance = roadDict[each][1]
if distance < oldDistance:
roadDict[each] = [point,distance]
else:
roadList.append(each)
roadDict[each] = [point,distance]
#反推出路径
def getroad():
road = [end]
node = end
while True:
nextnode = roadDict.get(node)[0]
road.append(nextnode)
node = nextnode
if nextnode == start:
break
road.reverse()
return road
roadDict = {start:[start,0]}
roadList = [start]
#这个遍历是实时更新的,不安全。
for node in roadList:
if node != end:
spfa(node)
result = getroad()
return result
基于spfa思想,结合程序本身。我自己编写了一个简化版的spfa代码,不同于网上的spfa代码(主要是我不太看得懂,且没有耐心研读....)。
总结
solutions.py 看似是一个算法集合,但是自我将spfa算法放进去之后,经过测试,除了spfa,其他的算法我都看不上了(简直瞧不起自己),算法一的优化存在极大的问题,在某些(很多)情况下,1.5倍的两直线距离卡递归深度是简陋的,是极不稳定的,是跑不出来结果的。而算法二的直接寻路,局部最优的思想得到的并不一定是全局最优的结果,也就是说,他虽然在任何情况下都能跑出来结果,但是规划得到的路径不一定是最短路径,最优路径。而当前两个算法结合之后,以算法二寻得的次优路径值作为递归深度的阈值,计算速度还是相当可观的,计算结果也是全局最优的。
但是,but,but,but,spfa算法,不论是计算速度和计算结果,都是最优的,相比于算法一和算法二的结合,spfa的速断还是更快。毕竟虽然卡了递归深度,但是仍然要进行算法一的众多递归,而且先执行算法二寻找出一条可行的次优路径就已经浪费掉了时间,而之后又要再寻找一次最优路径,就相当于是执行了两次寻路算法,逻辑上都比spfa慢2倍,更别说递归的时间复杂度不是线性的。
因此以后的实验,都会选择用spfa来实现。
转载请注明出处:https://www.cnblogs.com/dragonbean/p/13498421.html