权重的初始化:
1.如果激活函数是:Relu: W(n[L],n[L-1])=np.random.rand(n[L],n[L-1]) *np.sqrt(2/n[L-1])
2.如果激活函数是:tanh: W(n[L],n[L-1])=np.random.rand(n[L],n[L-1]) *np.sqrt(1/n[L-1])
1 def initialize_parameters_he(layers_dims): 2 """ 3 Arguments: 4 layer_dims -- python array (list) containing the size of each layer. 5 6 Returns: 7 parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": 8 W1 -- weight matrix of shape (layers_dims[1], layers_dims[0]) 9 b1 -- bias vector of shape (layers_dims[1], 1) 10 ... 11 WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1]) 12 bL -- bias vector of shape (layers_dims[L], 1) 13 """ 14 15 np.random.seed(3) 16 parameters = {} 17 L = len(layers_dims) - 1 # integer representing the number of layers 18 19 for l in range(1, L + 1): 20 ### START CODE HERE ### (≈ 2 lines of code) 21 parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1])*np.sqrt(1/layers_dims[l-1]) 22 parameters['b' + str(l)] = np.zeros((layers_dims[l],1)) 23 ### END CODE HERE ### 24 25 return parameters
正则化:
L2 Regularization : The standard way to avoid overfitting
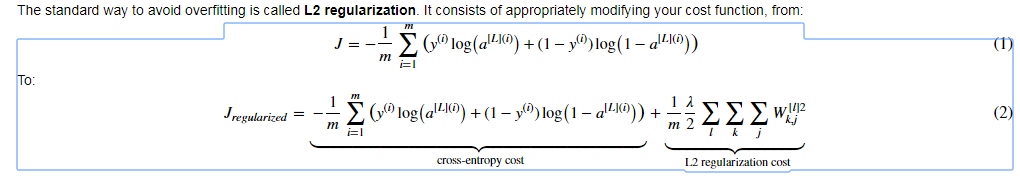
1. Basic function:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import h5py 4 import sklearn 5 import sklearn.datasets 6 import sklearn.linear_model 7 import scipy.io 8 9 def sigmoid(x): 10 """ 11 Compute the sigmoid of x 12 13 Arguments: 14 x -- A scalar or numpy array of any size. 15 16 Return: 17 s -- sigmoid(x) 18 """ 19 s = 1/(1+np.exp(-x)) 20 return s 21 22 def relu(x): 23 """ 24 Compute the relu of x 25 26 Arguments: 27 x -- A scalar or numpy array of any size. 28 29 Return: 30 s -- relu(x) 31 """ 32 s = np.maximum(0,x) 33 34 return s 35 36 def load_planar_dataset(seed): 37 38 np.random.seed(seed) 39 40 m = 400 # number of examples 41 N = int(m/2) # number of points per class 42 D = 2 # dimensionality 43 X = np.zeros((m,D)) # data matrix where each row is a single example 44 Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue) 45 a = 4 # maximum ray of the flower 46 47 for j in range(2): 48 ix = range(N*j,N*(j+1)) 49 t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta 50 r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius 51 X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] 52 Y[ix] = j 53 54 X = X.T 55 Y = Y.T 56 57 return X, Y 58 59 def initialize_parameters(layer_dims): 60 """ 61 Arguments: 62 layer_dims -- python array (list) containing the dimensions of each layer in our network 63 64 Returns: 65 parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": 66 W1 -- weight matrix of shape (layer_dims[l], layer_dims[l-1]) 67 b1 -- bias vector of shape (layer_dims[l], 1) 68 Wl -- weight matrix of shape (layer_dims[l-1], layer_dims[l]) 69 bl -- bias vector of shape (1, layer_dims[l]) 70 71 Tips: 72 - For example: the layer_dims for the "Planar Data classification model" would have been [2,2,1]. 73 This means W1's shape was (2,2), b1 was (1,2), W2 was (2,1) and b2 was (1,1). Now you have to generalize it! 74 - In the for loop, use parameters['W' + str(l)] to access Wl, where l is the iterative integer. 75 """ 76 77 np.random.seed(3) 78 parameters = {} 79 L = len(layer_dims) # number of layers in the network 80 81 for l in range(1, L): 82 parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) / np.sqrt(layer_dims[l-1]) 83 parameters['b' + str(l)] = np.zeros((layer_dims[l], 1)) 84 85 assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-1]) 86 assert(parameters['W' + str(l)].shape == layer_dims[l], 1) 87 88 89 return parameters 90 91 def forward_propagation(X, parameters): 92 """ 93 Implements the forward propagation (and computes the loss) presented in Figure 2. 94 95 Arguments: 96 X -- input dataset, of shape (input size, number of examples) 97 parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3": 98 W1 -- weight matrix of shape () 99 b1 -- bias vector of shape () 100 W2 -- weight matrix of shape () 101 b2 -- bias vector of shape () 102 W3 -- weight matrix of shape () 103 b3 -- bias vector of shape () 104 105 Returns: 106 loss -- the loss function (vanilla logistic loss) 107 """ 108 109 # retrieve parameters 110 W1 = parameters["W1"] 111 b1 = parameters["b1"] 112 W2 = parameters["W2"] 113 b2 = parameters["b2"] 114 W3 = parameters["W3"] 115 b3 = parameters["b3"] 116 117 # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID 118 Z1 = np.dot(W1, X) + b1 119 A1 = relu(Z1) 120 Z2 = np.dot(W2, A1) + b2 121 A2 = relu(Z2) 122 Z3 = np.dot(W3, A2) + b3 123 A3 = sigmoid(Z3) 124 125 cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) 126 127 return A3, cache 128 129 def backward_propagation(X, Y, cache): 130 """ 131 Implement the backward propagation presented in figure 2. 132 133 Arguments: 134 X -- input dataset, of shape (input size, number of examples) 135 Y -- true "label" vector (containing 0 if cat, 1 if non-cat) 136 cache -- cache output from forward_propagation() 137 138 Returns: 139 gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables 140 """ 141 m = X.shape[1] 142 (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache 143 144 dZ3 = A3 - Y 145 dW3 = 1./m * np.dot(dZ3, A2.T) 146 db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True) 147 148 dA2 = np.dot(W3.T, dZ3) 149 dZ2 = np.multiply(dA2, np.int64(A2 > 0)) 150 dW2 = 1./m * np.dot(dZ2, A1.T) 151 db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True) 152 153 dA1 = np.dot(W2.T, dZ2) 154 dZ1 = np.multiply(dA1, np.int64(A1 > 0)) 155 dW1 = 1./m * np.dot(dZ1, X.T) 156 db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True) 157 158 gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, 159 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2, 160 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1} 161 162 return gradients 163 164 def update_parameters(parameters, grads, learning_rate): 165 """ 166 Update parameters using gradient descent 167 168 Arguments: 169 parameters -- python dictionary containing your parameters: 170 parameters['W' + str(i)] = Wi 171 parameters['b' + str(i)] = bi 172 grads -- python dictionary containing your gradients for each parameters: 173 grads['dW' + str(i)] = dWi 174 grads['db' + str(i)] = dbi 175 learning_rate -- the learning rate, scalar. 176 177 Returns: 178 parameters -- python dictionary containing your updated parameters 179 """ 180 181 n = len(parameters) // 2 # number of layers in the neural networks 182 183 # Update rule for each parameter 184 for k in range(n): 185 parameters["W" + str(k+1)] = parameters["W" + str(k+1)] - learning_rate * grads["dW" + str(k+1)] 186 parameters["b" + str(k+1)] = parameters["b" + str(k+1)] - learning_rate * grads["db" + str(k+1)] 187 188 return parameters 189 190 def predict(X, y, parameters): 191 """ 192 This function is used to predict the results of a n-layer neural network. 193 194 Arguments: 195 X -- data set of examples you would like to label 196 parameters -- parameters of the trained model 197 198 Returns: 199 p -- predictions for the given dataset X 200 """ 201 202 m = X.shape[1] 203 p = np.zeros((1,m), dtype = np.int) 204 205 # Forward propagation 206 a3, caches = forward_propagation(X, parameters) 207 208 # convert probas to 0/1 predictions 209 for i in range(0, a3.shape[1]): 210 if a3[0,i] > 0.5: 211 p[0,i] = 1 212 else: 213 p[0,i] = 0 214 215 # print results 216 217 #print ("predictions: " + str(p[0,:])) 218 #print ("true labels: " + str(y[0,:])) 219 print("Accuracy: " + str(np.mean((p[0,:] == y[0,:])))) 220 221 return p 222 223 def compute_cost(a3, Y): 224 """ 225 Implement the cost function 226 227 Arguments: 228 a3 -- post-activation, output of forward propagation 229 Y -- "true" labels vector, same shape as a3 230 231 Returns: 232 cost - value of the cost function 233 """ 234 m = Y.shape[1] 235 236 logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y) 237 cost = 1./m * np.nansum(logprobs) 238 239 return cost 240 241 def load_dataset(): 242 train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r") 243 train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features 244 train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels 245 246 test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r") 247 test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features 248 test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels 249 250 classes = np.array(test_dataset["list_classes"][:]) # the list of classes 251 252 train_set_y = train_set_y_orig.reshape((1, train_set_y_orig.shape[0])) 253 test_set_y = test_set_y_orig.reshape((1, test_set_y_orig.shape[0])) 254 255 train_set_x_orig = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T 256 test_set_x_orig = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T 257 258 train_set_x = train_set_x_orig/255 259 test_set_x = test_set_x_orig/255 260 261 return train_set_x, train_set_y, test_set_x, test_set_y, classes 262 263 264 def predict_dec(parameters, X): 265 """ 266 Used for plotting decision boundary. 267 268 Arguments: 269 parameters -- python dictionary containing your parameters 270 X -- input data of size (m, K) 271 272 Returns 273 predictions -- vector of predictions of our model (red: 0 / blue: 1) 274 """ 275 276 # Predict using forward propagation and a classification threshold of 0.5 277 a3, cache = forward_propagation(X, parameters) 278 predictions = (a3>0.5) 279 return predictions 280 281 def load_planar_dataset(randomness, seed): 282 283 np.random.seed(seed) 284 285 m = 50 286 N = int(m/2) # number of points per class 287 D = 2 # dimensionality 288 X = np.zeros((m,D)) # data matrix where each row is a single example 289 Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue) 290 a = 2 # maximum ray of the flower 291 292 for j in range(2): 293 294 ix = range(N*j,N*(j+1)) 295 if j == 0: 296 t = np.linspace(j, 4*3.1415*(j+1),N) #+ np.random.randn(N)*randomness # theta 297 r = 0.3*np.square(t) + np.random.randn(N)*randomness # radius 298 if j == 1: 299 t = np.linspace(j, 2*3.1415*(j+1),N) #+ np.random.randn(N)*randomness # theta 300 r = 0.2*np.square(t) + np.random.randn(N)*randomness # radius 301 302 X[ix] = np.c_[r*np.cos(t), r*np.sin(t)] 303 Y[ix] = j 304 305 X = X.T 306 Y = Y.T 307 308 return X, Y 309 310 def plot_decision_boundary(model, X, y): 311 # Set min and max values and give it some padding 312 x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1 313 y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1 314 h = 0.01 315 # Generate a grid of points with distance h between them 316 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) 317 # Predict the function value for the whole grid 318 Z = model(np.c_[xx.ravel(), yy.ravel()]) 319 Z = Z.reshape(xx.shape) 320 # Plot the contour and training examples 321 plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral) 322 plt.ylabel('x2') 323 plt.xlabel('x1') 324 plt.scatter(X[0, :], X[1, :], c=np.squeeze(y), cmap=plt.cm.Spectral) 325 plt.show() 326 327 def load_2D_dataset(): 328 data = scipy.io.loadmat('datasets/data.mat') 329 train_X = data['X'].T 330 train_Y = data['y'].T 331 test_X = data['Xval'].T 332 test_Y = data['yval'].T 333 334 #plt.scatter(train_X[0, :], train_X[1, :], c=np.squeeze(train_Y), s=40, cmap=plt.cm.Spectral); 335 336 return train_X, train_Y, test_X, test_Y
2. Build Model
1 def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1): 2 """ 3 Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID. 4 5 Arguments: 6 X -- input data, of shape (input size, number of examples) 7 Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples) 8 learning_rate -- learning rate of the optimization 9 num_iterations -- number of iterations of the optimization loop 10 print_cost -- If True, print the cost every 10000 iterations 11 lambd -- regularization hyperparameter, scalar 12 keep_prob - probability of keeping a neuron active during drop-out, scalar. 13 14 Returns: 15 parameters -- parameters learned by the model. They can then be used to predict. 16 """ 17 18 grads = {} 19 costs = [] # to keep track of the cost 20 m = X.shape[1] # number of examples 21 layers_dims = [X.shape[0], 20, 3, 1] 22 23 # Initialize parameters dictionary. 24 parameters = initialize_parameters(layers_dims) 25 26 # Loop (gradient descent) 27 28 for i in range(0, num_iterations): 29 30 # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID. 31 if keep_prob == 1: 32 a3, cache = forward_propagation(X, parameters) 33 elif keep_prob < 1: 34 a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob) 35 36 # Cost function 37 if lambd == 0: 38 cost = compute_cost(a3, Y) 39 else: 40 cost = compute_cost_with_regularization(a3, Y, parameters, lambd) 41 42 # Backward propagation. 43 assert(lambd==0 or keep_prob==1) # it is possible to use both L2 regularization and dropout, 44 # but this assignment will only explore one at a time 45 if lambd == 0 and keep_prob == 1: 46 grads = backward_propagation(X, Y, cache) 47 elif lambd != 0: 48 grads = backward_propagation_with_regularization(X, Y, cache, lambd) 49 elif keep_prob < 1: 50 grads = backward_propagation_with_dropout(X, Y, cache, keep_prob) 51 52 # Update parameters. 53 parameters = update_parameters(parameters, grads, learning_rate) 54 55 # Print the loss every 10000 iterations 56 if print_cost and i % 10000 == 0: 57 print("Cost after iteration {}: {}".format(i, cost)) 58 if print_cost and i % 1000 == 0: 59 costs.append(cost) 60 61 # plot the cost 62 plt.plot(costs) 63 plt.ylabel('cost') 64 plt.xlabel('iterations (x1,000)') 65 plt.title("Learning rate =" + str(learning_rate)) 66 plt.show() 67 68 return parameters
3. Build without any regularzation
1 parameters = model(train_X, train_Y) 2 print ("On the training set:") 3 predictions_train = predict(train_X, train_Y, parameters) 4 print ("On the test set:") 5 predictions_test = predict(test_X, test_Y, parameters) 6 plt.title("Model without regularization") 7 axes = plt.gca() 8 axes.set_xlim([-0.75,0.40]) 9 axes.set_ylim([-0.75,0.65]) 10 plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
4. Build model with L2 regularzation:
1 #L2 regularization compute_cost function: 2 3 def compute_cost_with_regularization(A3, Y, parameters, lambd): 4 """ 5 Implement the cost function with L2 regularization. See formula (2) above. 6 7 Arguments: 8 A3 -- post-activation, output of forward propagation, of shape (output size, number of examples) 9 Y -- "true" labels vector, of shape (output size, number of examples) 10 parameters -- python dictionary containing parameters of the model 11 12 Returns: 13 cost - value of the regularized loss function (formula (2)) 14 """ 15 m = Y.shape[1] 16 W1 = parameters["W1"] 17 W2 = parameters["W2"] 18 W3 = parameters["W3"] 19 20 cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost 21 22 ### START CODE HERE ### (approx. 1 line) 23 L2_regularization_cost = (1.0/(2*m))*lambd*(np.sum(np.square(W1))+np.sum(np.square(W2))+np.sum(np.square(W3))) 24 ### END CODER HERE ### 25 26 cost = cross_entropy_cost + L2_regularization_cost 27 28 return cost 29 30 # L2 backward_propagation regularization: 31 32 def backward_propagation_with_regularization(X, Y, cache, lambd): 33 """ 34 Implements the backward propagation of our baseline model to which we added an L2 regularization. 35 36 Arguments: 37 X -- input dataset, of shape (input size, number of examples) 38 Y -- "true" labels vector, of shape (output size, number of examples) 39 cache -- cache output from forward_propagation() 40 lambd -- regularization hyperparameter, scalar 41 42 Returns: 43 gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables 44 """ 45 46 m = X.shape[1] 47 (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache 48 49 dZ3 = A3 - Y 50 51 ### START CODE HERE ### (approx. 1 line) 52 dW3 = 1./m * np.dot(dZ3, A2.T) + (lambd/m)*W3 53 ### END CODE HERE ### 54 db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True) 55 56 dA2 = np.dot(W3.T, dZ3) 57 dZ2 = np.multiply(dA2, np.int64(A2 > 0)) 58 ### START CODE HERE ### (approx. 1 line) 59 dW2 = 1./m * np.dot(dZ2, A1.T) + (lambd/m)*W2 60 ### END CODE HERE ### 61 db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True) 62 63 dA1 = np.dot(W2.T, dZ2) 64 dZ1 = np.multiply(dA1, np.int64(A1 > 0)) 65 ### START CODE HERE ### (approx. 1 line) 66 dW1 = 1./m * np.dot(dZ1, X.T) + (lambd/m)*W1 67 ### END CODE HERE ### 68 db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True) 69 70 gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2, 71 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 72 "dZ1": dZ1, "dW1": dW1, "db1": db1} 73 74 return gradients 75 76 #Build with L2 regularization model: 77 parameters = model(train_X, train_Y, lambd = 0.7) 78 print ("On the train set:") 79 predictions_train = predict(train_X, train_Y, parameters) 80 print ("On the test set:") 81 predictions_test = predict(test_X, test_Y, parameters) 82 plt.title("Model with L2-regularization") 83 axes = plt.gca() 84 axes.set_xlim([-0.75,0.40]) 85 axes.set_ylim([-0.75,0.65]) 86 plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
Observations:
- The value of λ is a hyperparameter that you can tune using a dev set.
- L2 regularization makes your decision boundary smoother. If λ is too large, it is also possible to "oversmooth", resulting in a model with high bias.
What is L2-regularization actually doing?:
L2-regularization relies on the assumption that a model with small weights is simpler than a model with large weights. Thus, by penalizing the square values of the weights in the cost function you drive all the weights to smaller values. It becomes too costly for the cost to have large weights! This leads to a smoother model in which the output changes more slowly as the input changes.
**What you should remember** -- the implications of L2-regularization on: - The cost computation: - A regularization term is added to the cost - The backpropagation function: - There are extra terms in the gradients with respect to weight matrices - Weights end up smaller ("weight decay"): - Weights are pushed to smaller values.
5. Build modle with Dropout
Dropout is a widely used regularization technique that is specific to deep learning. It randomly shuts down some neurons in each iteration,
You shut down each neuron of a layer with probability 1-keep_prob or keep it with probability keep_prob.The dropped neurons don't contribute to the training in both the forward and backward propagations of the iteration. When you shut some neurons down,you actually modify your model ,you train a different model that uses only a subset of your neurons.
5.1 Forward propagation with dropout:
We just add dropout to the hidden layers, not apply dropout to the input layer or output layer.
1 def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5): 2 """ 3 Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID. 4 5 Arguments: 6 X -- input dataset, of shape (2, number of examples) 7 parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3": 8 W1 -- weight matrix of shape (20, 2) 9 b1 -- bias vector of shape (20, 1) 10 W2 -- weight matrix of shape (3, 20) 11 b2 -- bias vector of shape (3, 1) 12 W3 -- weight matrix of shape (1, 3) 13 b3 -- bias vector of shape (1, 1) 14 keep_prob - probability of keeping a neuron active during drop-out, scalar 15 16 Returns: 17 A3 -- last activation value, output of the forward propagation, of shape (1,1) 18 cache -- tuple, information stored for computing the backward propagation 19 """ 20 21 np.random.seed(1) 22 23 # retrieve parameters 24 W1 = parameters["W1"] 25 b1 = parameters["b1"] 26 W2 = parameters["W2"] 27 b2 = parameters["b2"] 28 W3 = parameters["W3"] 29 b3 = parameters["b3"] 30 31 # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID 32 Z1 = np.dot(W1, X) + b1 33 A1 = relu(Z1) 34 ### START CODE HERE ### (approx. 4 lines) # Steps 1-4 below correspond to the Steps 1-4 described above. 35 D1 = np.random.rand(A1.shape[0],A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...) 36 D1 = (D1<keep_prob) # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold) 37 A1 = A1*D1 # Step 3: shut down some neurons of A1 38 A1 = A1/keep_prob # Step 4: scale the value of neurons that haven't been shut down 39 ### END CODE HERE ### 40 Z2 = np.dot(W2, A1) + b2 41 A2 = relu(Z2) 42 ### START CODE HERE ### (approx. 4 lines) 43 D2 = np.random.rand(A2.shape[0],A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...) 44 D2 = (D2<keep_prob) # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold) 45 A2 = A2*D2 # Step 3: shut down some neurons of A2 46 A2 = A2/keep_prob # Step 4: scale the value of neurons that haven't been shut down 47 ### END CODE HERE ### 48 Z3 = np.dot(W3, A2) + b3 49 A3 = sigmoid(Z3) 50 51 cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) 52 53 return A3, cache
5.2 Backward propagation with dropout:
1 def backward_propagation_with_dropout(X, Y, cache, keep_prob): 2 """ 3 Implements the backward propagation of our baseline model to which we added dropout. 4 5 Arguments: 6 X -- input dataset, of shape (2, number of examples) 7 Y -- "true" labels vector, of shape (output size, number of examples) 8 cache -- cache output from forward_propagation_with_dropout() 9 keep_prob - probability of keeping a neuron active during drop-out, scalar 10 11 Returns: 12 gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables 13 """ 14 15 m = X.shape[1] 16 (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache 17 18 dZ3 = A3 - Y 19 dW3 = 1./m * np.dot(dZ3, A2.T) 20 db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True) 21 dA2 = np.dot(W3.T, dZ3) 22 ### START CODE HERE ### (≈ 2 lines of code) 23 dA2 = dA2*D2 # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation 24 dA2 = dA2/keep_prob # Step 2: Scale the value of neurons that haven't been shut down 25 ### END CODE HERE ### 26 dZ2 = np.multiply(dA2, np.int64(A2 > 0)) 27 dW2 = 1./m * np.dot(dZ2, A1.T) 28 db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True) 29 30 dA1 = np.dot(W2.T, dZ2) 31 ### START CODE HERE ### (≈ 2 lines of code) 32 dA1 = dA1*D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation 33 dA1 = dA1/keep_prob # Step 2: Scale the value of neurons that haven't been shut down 34 ### END CODE HERE ### 35 dZ1 = np.multiply(dA1, np.int64(A1 > 0)) 36 dW1 = 1./m * np.dot(dZ1, X.T) 37 db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True) 38 39 gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2, 40 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 41 "dZ1": dZ1, "dW1": dW1, "db1": db1} 42 43 return gradients
5.3 Build model with dropout :
1 parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3) 2 3 print ("On the train set:") 4 predictions_train = predict(train_X, train_Y, parameters) 5 print ("On the test set:") 6 predictions_test = predict(test_X, test_Y, parameters) 7 plt.title("Model with dropout") 8 axes = plt.gca() 9 axes.set_xlim([-0.75,0.40]) 10 axes.set_ylim([-0.75,0.65]) 11 plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
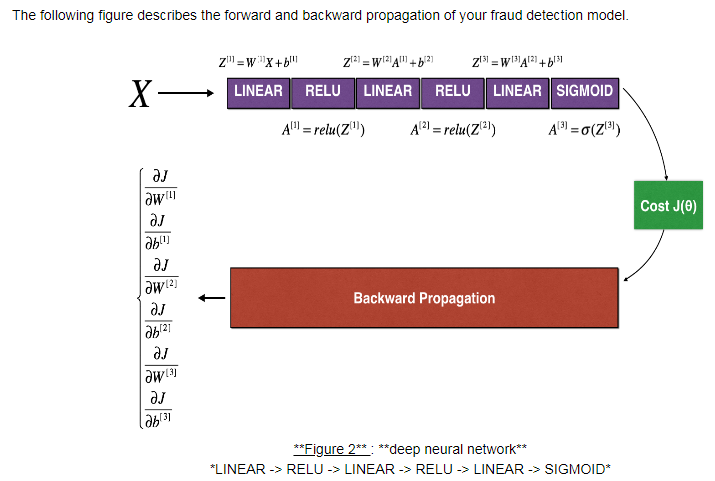
6. Gradient Checking:
f'=(f(x+e)-f(x-e))/2e 双边误差 e逼近无穷小





1 #forward_propagation function 2 def forward_propagation(x, theta): 3 """ 4 Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x) 5 6 Arguments: 7 x -- a real-valued input 8 theta -- our parameter, a real number as well 9 10 Returns: 11 J -- the value of function J, computed using the formula J(theta) = theta * x 12 """ 13 14 ### START CODE HERE ### (approx. 1 line) 15 J = np.multiply(x,theta) 16 ### END CODE HERE ### 17 18 return J 19 20 #backward_propagation function: 21 22 def backward_propagation(x, theta): 23 """ 24 Computes the derivative of J with respect to theta (see Figure 1). 25 26 Arguments: 27 x -- a real-valued input 28 theta -- our parameter, a real number as well 29 30 Returns: 31 dtheta -- the gradient of the cost with respect to theta 32 """ 33 34 ### START CODE HERE ### (approx. 1 line) 35 dtheta = x 36 ### END CODE HERE ### 37 38 return dtheta 39 40 #gradient_check function: 41 def gradient_check(x, theta, epsilon = 1e-7): 42 """ 43 Implement the backward propagation presented in Figure 1. 44 45 Arguments: 46 x -- a real-valued input 47 theta -- our parameter, a real number as well 48 epsilon -- tiny shift to the input to compute approximated gradient with formula(1) 49 50 Returns: 51 difference -- difference (2) between the approximated gradient and the backward propagation gradient 52 """ 53 54 # Compute gradapprox using left side of formula (1). epsilon is small enough, you don't need to worry about the limit. 55 ### START CODE HERE ### (approx. 5 lines) 56 thetaplus = theta+epsilon # Step 1 57 thetaminus = theta-epsilon # Step 2 58 J_plus = forward_propagation(x,thetaplus) # Step 3 59 J_minus = forward_propagation(x,thetaminus) # Step 4 60 gradapprox = (J_plus-J_minus)/(2*epsilon) # Step 5 61 ### END CODE HERE ### 62 63 # Check if gradapprox is close enough to the output of backward_propagation() 64 ### START CODE HERE ### (approx. 1 line) 65 grad = backward_propagation(x,theta) 66 ### END CODE HERE ### 67 68 ### START CODE HERE ### (approx. 1 line) 69 numerator = np.linalg.norm(grad-gradapprox) # Step 1' 70 denominator = np.linalg.norm(grad)+np.linalg.norm(gradapprox) # Step 2' 71 difference = numerator/denominator # Step 3' 72 ### END CODE HERE ### 73 74 if difference < 1e-7: 75 print ("The gradient is correct!") 76 else: 77 print ("The gradient is wrong!") 78 79 return difference
N-dimensional gradient checking:
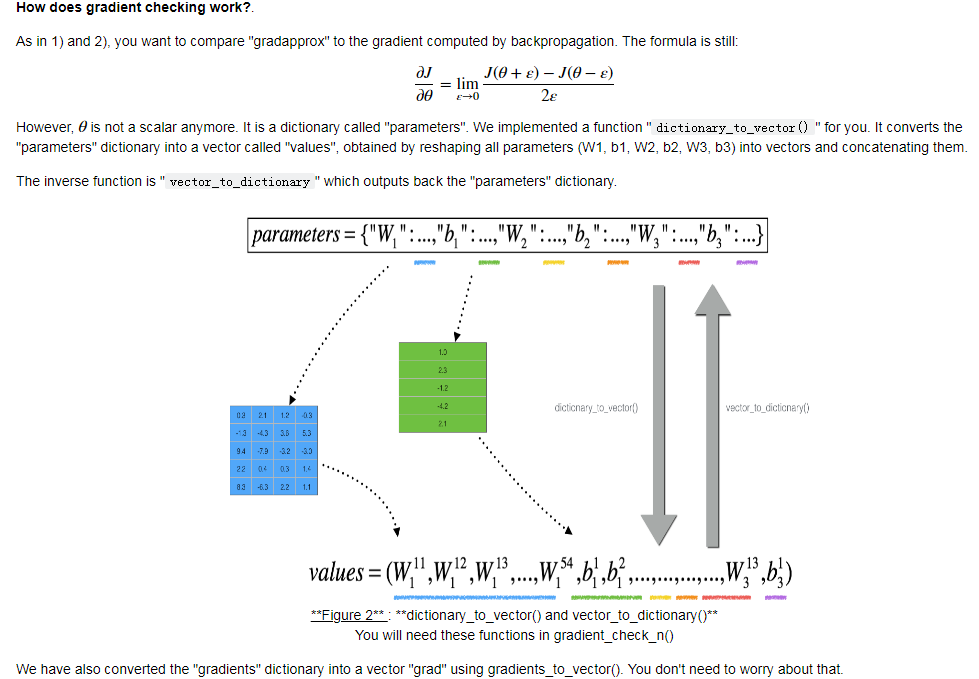

1 def forward_propagation_n(X, Y, parameters): 2 """ 3 Implements the forward propagation (and computes the cost) presented in Figure 3. 4 5 Arguments: 6 X -- training set for m examples 7 Y -- labels for m examples 8 parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3": 9 W1 -- weight matrix of shape (5, 4) 10 b1 -- bias vector of shape (5, 1) 11 W2 -- weight matrix of shape (3, 5) 12 b2 -- bias vector of shape (3, 1) 13 W3 -- weight matrix of shape (1, 3) 14 b3 -- bias vector of shape (1, 1) 15 16 Returns: 17 cost -- the cost function (logistic cost for one example) 18 """ 19 20 # retrieve parameters 21 m = X.shape[1] 22 W1 = parameters["W1"] 23 b1 = parameters["b1"] 24 W2 = parameters["W2"] 25 b2 = parameters["b2"] 26 W3 = parameters["W3"] 27 b3 = parameters["b3"] 28 29 # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID 30 Z1 = np.dot(W1, X) + b1 31 A1 = relu(Z1) 32 Z2 = np.dot(W2, A1) + b2 33 A2 = relu(Z2) 34 Z3 = np.dot(W3, A2) + b3 35 A3 = sigmoid(Z3) 36 37 # Cost 38 logprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y) 39 cost = 1./m * np.sum(logprobs) 40 41 cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) 42 43 return cost, cache 44 45 def backward_propagation_n(X, Y, cache): 46 """ 47 Implement the backward propagation presented in figure 2. 48 49 Arguments: 50 X -- input datapoint, of shape (input size, 1) 51 Y -- true "label" 52 cache -- cache output from forward_propagation_n() 53 54 Returns: 55 gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables. 56 """ 57 58 m = X.shape[1] 59 (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache 60 61 dZ3 = A3 - Y 62 dW3 = 1./m * np.dot(dZ3, A2.T) 63 db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True) 64 65 dA2 = np.dot(W3.T, dZ3) 66 dZ2 = np.multiply(dA2, np.int64(A2 > 0)) 67 dW2 = 1./m * np.dot(dZ2, A1.T) * 2 68 db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True) 69 70 dA1 = np.dot(W2.T, dZ2) 71 dZ1 = np.multiply(dA1, np.int64(A1 > 0)) 72 dW1 = 1./m * np.dot(dZ1, X.T) 73 db1 = 4./m * np.sum(dZ1, axis=1, keepdims = True) 74 75 gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, 76 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2, 77 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1} 78 79 return gradients 80 81 82 def dictionary_to_vector(parameters): 83 """ 84 Roll all our parameters dictionary into a single vector satisfying our specific required shape. 85 """ 86 keys = [] 87 count = 0 88 for key in ["W1", "b1", "W2", "b2", "W3", "b3"]: 89 90 # flatten parameter 91 new_vector = np.reshape(parameters[key], (-1,1)) 92 keys = keys + [key]*new_vector.shape[0] 93 94 if count == 0: 95 theta = new_vector 96 else: 97 theta = np.concatenate((theta, new_vector), axis=0) 98 count = count + 1 99 100 return theta, keys 101 102 def vector_to_dictionary(theta): 103 """ 104 Unroll all our parameters dictionary from a single vector satisfying our specific required shape. 105 """ 106 parameters = {} 107 parameters["W1"] = theta[:20].reshape((5,4)) 108 parameters["b1"] = theta[20:25].reshape((5,1)) 109 parameters["W2"] = theta[25:40].reshape((3,5)) 110 parameters["b2"] = theta[40:43].reshape((3,1)) 111 parameters["W3"] = theta[43:46].reshape((1,3)) 112 parameters["b3"] = theta[46:47].reshape((1,1)) 113 114 return parameters 115 def gradients_to_vector(gradients): 116 """ 117 Roll all our gradients dictionary into a single vector satisfying our specific required shape. 118 """ 119 120 count = 0 121 for key in ["dW1", "db1", "dW2", "db2", "dW3", "db3"]: 122 # flatten parameter 123 new_vector = np.reshape(gradients[key], (-1,1)) 124 125 if count == 0: 126 theta = new_vector 127 else: 128 theta = np.concatenate((theta, new_vector), axis=0) 129 count = count + 1 130 131 return theta 132 133 def gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7): 134 """ 135 Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n 136 137 Arguments: 138 parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3": 139 grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters. 140 x -- input datapoint, of shape (input size, 1) 141 y -- true "label" 142 epsilon -- tiny shift to the input to compute approximated gradient with formula(1) 143 144 Returns: 145 difference -- difference (2) between the approximated gradient and the backward propagation gradient 146 """ 147 148 # Set-up variables 149 parameters_values, _ = dictionary_to_vector(parameters) 150 grad = gradients_to_vector(gradients) 151 num_parameters = parameters_values.shape[0] 152 J_plus = np.zeros((num_parameters, 1)) 153 J_minus = np.zeros((num_parameters, 1)) 154 gradapprox = np.zeros((num_parameters, 1)) 155 156 # Compute gradapprox 157 for i in range(num_parameters): 158 159 # Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]". 160 # "_" is used because the function you have to outputs two parameters but we only care about the first one 161 ### START CODE HERE ### (approx. 3 lines) 162 thetaplus = np.copy(parameters_values) # Step 1 163 thetaplus[i][0] =thetaplus[i][0]+epsilon # Step 2 164 J_plus[i], _ =forward_propagation_n(X,Y,vector_to_dictionary(thetaplus)) # Step 3 165 ### END CODE HERE ### 166 167 # Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]". 168 ### START CODE HERE ### (approx. 3 lines) 169 thetaminus = np.copy(parameters_values) # Step 1 170 thetaminus[i][0] = thetaminus[i][0]-epsilon # Step 2 171 J_minus[i], _ = forward_propagation_n(X,Y,vector_to_dictionary(thetaminus)) # Step 3 172 ### END CODE HERE ### 173 174 # Compute gradapprox[i] 175 ### START CODE HERE ### (approx. 1 line) 176 gradapprox[i] = (J_plus[i]-J_minus[i])/(2*epsilon) 177 ### END CODE HERE ### 178 179 # Compare gradapprox to backward propagation gradients by computing difference. 180 ### START CODE HERE ### (approx. 1 line) 181 numerator = np.linalg.norm(gradients_to_vector(gradients)-gradapprox) # Step 1' 182 denominator = np.linalg.norm(gradients_to_vector(gradients))+np.linalg.norm(gradapprox) # Step 2' 183 difference = numerator/denominator # Step 3' 184 ### END CODE HERE ### 185 186 if difference > 1e-7: 187 print ("�33[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "�33[0m") 188 else: 189 print ("�33[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "�33[0m") 190 191 return difference