zoukankan      html  css  js  c++  java

  • 红黑数之原理分析及C语言实现

    目录：

    　　1.红黑树简介（概念，特征，用途）

    　　2.红黑树的C语言实现（树形结构，添加，旋转）

    　　3.部分面试题（）

    1.红黑树简介

    　1.1 红黑树概念

    　　红黑树(Red-Black Tree，简称R-B Tree)是一棵特殊的二叉搜索树（任意一个节点所包含的键值，大于等于左孩子的键值，小于等于右孩子的键值）。

    　　它在每个结点上增加了一个存储位来表示结点的颜色，可以是RED或者BLACK。通过对一条从根节点到NIL叶节点（指空结点或者下面说的哨兵）的简单路径上各个结点在颜色进行约束，红黑树确保没有一条路径会比其他路径长出2倍，因而是近似平衡的。

    　1.2 红黑树特征

    　　1) 每个节点或者是黑色，或者是红色。
    　　(2) 根节点是黑色。
    　　(3) 每个叶子节点是黑色。 [注意：这里叶子节点，是指为空的叶子节点！]
    　　(4) 如果一个节点是红色的，则它的子节点必须是黑色的。
    　　(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

    　1.3 红黑树用途　

    　　红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保。对于查找、插入、删除、最大、最小等动态操作的时间复杂度为O(lgn).常见的用途有以下几种：

    • STL（标准模板库）中在set map是基于红黑树实现的。
    • epoll在内核中的实现，用红黑树管理事件块。
    • linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块

    2. 红黑树C语言实现

    　2.1 树形结构基本实现

    　　红黑树属于特殊的查找树，因此先对树形结构进行基本讲解。

    　　首先，树形结构有各个节点组成，节点的描述如下：

    struct  BTNode{
    int data；
    }；

    　　节点需要有自己的左右子孩子，因此需要两个指针

    typedef struct BTNode{
    int data；
    struct BTNode *lChild；
    struct BTNode *rChild；
}BiNode;

    　　对二叉树进行创建

    //先序创建

    int CreateBiTree(BiTNode **T)  
{  
    int ch;  
    scanf("%d",&ch);  
    if (ch == -1)  
    {  
        *T = NULL;  
        return 0;  
    }  
    else  
    {  
        *T = (BiTNode *)malloc(sizeof(BiTNode));  //为此节点申请内存空间，返回指针强制转换成BiNode*类型
        if (T == NULL)  
        {  
            printf("failed
");  
            return 0;  
        }  
        else  
        {  
            (*T)->data = ch;  
            printf("输入%d的左子节点：",ch);  
            CreateBiTree(&((*T)->lChild));  　　//递归方式存储左子节点数据
            printf("输入%d的右子节点：",ch);  
            CreateBiTree((&(*T)->rChild));  　　//递归方式存储右子节点数据
        }  
    }  
    return 1;  
}

    　　最开始时对二叉树的遍历难以理解，不过从算法中的递归角度进行理解将会简单很多。

    　　二叉树先序遍历

    void PreOrderBiTree(BiTNode *T)  
{  
    if (T == NULL)  
    {  
        return;  
    }  
    else  
    {  
        printf("%d ",T->data);  
        PreOrderBiTree(T->lChild);  
        PreOrderBiTree(T->rChild);  
    }  
}

    　　二叉树中序遍历

    void MiddleOrderBiTree(BiTNode *T)  
{  
    if (T == NULL)  
    {  
        return;  
    }  
    else  
    {  
        MiddleOrderBiTree(T->lChild);  
        printf("%d ",T->data);  
        MiddleOrderBiTree(T->rChild);  
    }  
}

    　　二叉树后序遍历

    void PostOrderBiTree(BiTNode *T)  
{  
    if (T == NULL)  
    {  
        return;  
    }  
    else  
    {  
        PostOrderBiTree(T->lChild);  
        PostOrderBiTree(T->rChild);  
        printf("%d ",T->data);  
    }  
}

    　　二叉树深度计算

    int TreeDeep(BiTNode *T)  
{  
    int deep = 0;  
    if (T != NULL)  
    {  
        int leftdeep = TreeDeep(T->lChild);  
        int rightdeep = TreeDeep(T->rChild);  
        deep = leftdeep >= rightdeep?leftdeep+1:rightdeep+1;  //从最后节开始，递归逐步后退，每退回一个节点 深度+1
    }  
  
    return deep;  
}

    　　二叉树叶子结点个数

    int LeafCount(BiTNode *T)  
{  
    static int count;  
    if (T != NULL)  
    {  
        if (T->lChild == NULL && T->rChild == NULL)  
        {  
            count++;  
        }  
  
        LeafCount(T->lChild);  
        LeafCount(T->rChild);  
    }  
  
    return count;  
}

    2.2 红黑树实现

    　　红黑树首先作为树的结构出现，包含了树形结构的基本特征，操作具有查找、添加、删除。在添加节点时必然导致红黑树的结构不符合红黑树规则，此时将对添加节点后的树进行旋转（左旋和右旋）以保证回复红黑树的特性。

    　　下面将以红黑树的旋转、添加、删除进行逐步讲解。

    　　红黑树基本节点定义

    #define RED      0    // 红色节点
#define BLACK    1    // 黑色节点

typedef int Type;

// 红黑树的节点
typedef struct RBTreeNode{
    unsigned char color;        // 颜色(RED 或 BLACK)
    Type   key;                    // 关键字(键值)
    struct RBTreeNode *left;    // 左孩子
    struct RBTreeNode *right;    // 右孩子
    struct RBTreeNode *parent;    // 父结点
}Node, *RBTree;

// 红黑树的根
typedef struct rb_root{
    Node *node;
}RBRoot;

    　　红黑树旋转

    　　　　这里写图片描述

    　　左旋（即上图从右到左）代码实现

    static void left_rotate(RBRoot *root, Node *x)
{
    // 设置x的右孩子为y
    Node *y = x->right;

    // 将 “y的左孩子” 设为 “x的右孩子”；
    // 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”
    x->right = y->left;
    if (y->left != NULL)
        y->left->parent = x;

    // 将 “x的父亲” 设为 “y的父亲”
    y->parent = x->parent;

    if (x->parent == NULL)
    {
        //tree = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点
        root->node = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点
    }
    else
    {
        if (x->parent->left == x)
            x->parent->left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
        else
            x->parent->right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
    }
    
    // 将 “x” 设为 “y的左孩子”
    y->left = x;
    // 将 “x的父节点” 设为 “y”
    x->parent = y;
}

    　　右旋（即上图从左向右）代码实现 

    static void rbtree_right_rotate(RBRoot *root, Node *y)
{
    // 设置x是当前节点的左孩子。
    Node *x = y->left;

    // 将 “x的右孩子” 设为 “y的左孩子”；
    // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”
    y->left = x->right;
    if (x->right != NULL)
        x->right->parent = y;

    // 将 “y的父亲” 设为 “x的父亲”
    x->parent = y->parent;

    if (y->parent == NULL) 
    {
        //tree = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点
        root->node = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点
    }
    else
    {
        if (y == y->parent->right)
            y->parent->right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
        else
            y->parent->left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
    }

    // 将 “y” 设为 “x的右孩子”
    x->right = y;

    // 将 “y的父节点” 设为 “x”
    y->parent = x;
}

    　　红黑树添加

    　　插入操作需要保证插入数据后红黑树的基本特征不被破坏，红黑树的5个基本特征复习一下：

    　　1) 每个节点或者是黑色，或者是红色。
    　　(2) 根节点是黑色。
    　　(3) 每个叶子节点是黑色。 [注意：这里叶子节点，是指为空的叶子节点！]
    　　(4) 如果一个节点是红色的，则它的子节点必须是黑色的。
    　　(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

    　　因此插入操作的关键在于以下几点：

    1. 新插入的节点一定是红色的。（如果是黑色的，会破坏条件5）
    2. 如果新插入的节点的父亲是黑色的，则没有破坏任何性质，那么插入完成。
    3. 如果插入节点的父节点是红色, 破坏了性质4. 故插入算法就是通过重新着色或旋转, 来维持性质

     　　插入新的数据（红色节点），一定要考虑他的叔叔的情况。并且，插入操作主要是维护颜色来保证树的平衡。将插入操作分为以下几种情况分别考虑：

    　　case 1. 如果插入的节点是根节点，也就是说初始的红黑树为空，这是最简单的情况，直接将该节点标识成黑色即可。

    　　　　　　 

    　　case 2. 如果新插入的节点不是红黑树的根节点，如果新插入的节点的父节点是黑色的话，那么红黑树是不需要调整的。

    　　　　　　　　 

    　　case 3. 如果新插入的节点的父节点是红色的话，显然这里违反了红黑树中不能存在父节点和子节点同时为红色的性质。

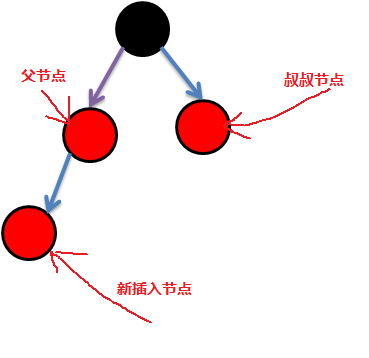
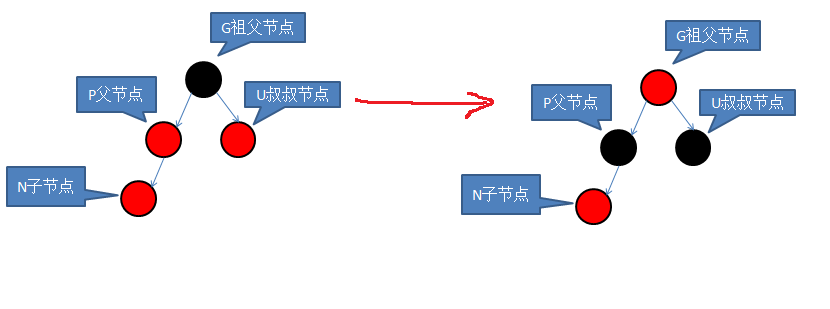
    　　　　　　叔节点为红色：修改祖父节点为红色，父节点及叔节点改为黑色。祖父节点再视为新加入节点与上层比对，保证红黑树不被破坏。

    　　　　　　　　 

    　　　　　　修改后：

    　　　　　　

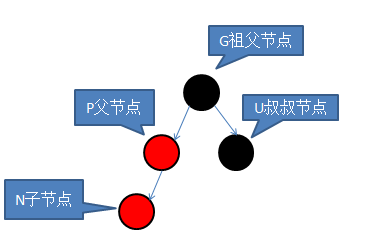
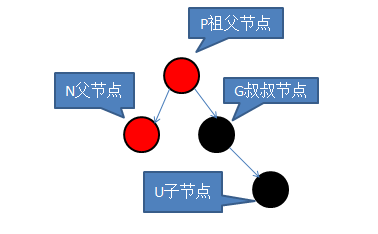
    　　　　　　叔节点为黑色：旋转，使父节点占据祖父节点位置，之后交换P与G的颜色：

    　　　　 

    　　　　　　旋转后：

    　　　　　　

    3.红黑树知识点

    　　3.1 红黑树和哈希表怎么选择？

    • 　　应该从多个方面分析：数据总量，空间消耗，查找效率
    • 　　查找效率：哈希表，常数时间不是吹的，这个和数据总量无关的，红黑树是logn级别的。（但是不一定选哪个，如果数量到达了一定的级别，哈希表还是比较好的，但是哈希表还有别的函数的消耗，这个也会影响）
    • 　　内存消耗：对内存消耗十分严格，最好是用红黑树，哈希表有可能会太大太难管理
    • 在实际的系统中，例如，需要使用动态规则的防火墙系统，使用红黑树而不是散列表被实践证明具有更好的伸缩性。Linux内核在管理vm_area_struct时就是采用了红黑树来维护内存块的。

    　　3.2 红黑树相比于BST和AVL树有什么优点？

    • 红黑树是牺牲了严格的高度平衡的优越条件为代价，它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。红黑树能够以O(log n)的时间复杂度进行搜索、插入、删除操作。此外，由于它的设计，任何不平衡都会在三次旋转之内解决。
    • 相比于BST（log（n+1）/log2），它的时间复杂度是更低的，而且最坏的时间复杂度是oN，这是不如红黑树的
    • 相比于AVL树，时间复杂度是相同的，但是红黑树的统计效率更高。其实选择哪个树主要是看插入的数据，插入的数据分布比较好则适合AVL，插入的数据比较混乱的话就适合红黑树了
    • 插入和删除操作（画图解释）
    • 左旋（将X变为左子节点），右旋操作（将Y变成右子节点）；插入（三种情况）删除（四种情况）操作。（画图解释原理）

    待续。。。
  • 相关阅读:
    vim命令总结
    SQL语句中----删除表数据drop、truncate和delete的用法
    备份数据工具类
    JavaWeb之 JSP：自定义标签
    Android studio安装与配置
    Redis 从入门到放弃
    java相关网址汇总2
    java相关网址汇总1
    校验字符串编码工具类
    java相关网址汇总(myself)
  • 原文地址：https://www.cnblogs.com/edver/p/7250313.html
Copyright © 2011-2022 走看看