【十大经典数据挖掘算法】EM

【十大经典数据挖掘算法】系列

1. C4.5
2. K-Means
3. SVM
4. Apriori
5. EM
6. PageRank
7. AdaBoost
8. kNN
9. Naïve Bayes
10. CART

---

1. 极大似然

极大似然（Maximum Likelihood）估计为用于已知模型的参数估计的统计学方法。比如，我们想了解抛硬币是正面（head）的概率分布( heta)；那么可以通过最大似然估计方法求得。假如我们抛硬币(10)次，其中(8)次正面、(2)次反面；极大似然估计参数( heta)值：

[hat{ heta} = argunderset{ heta}{max}\, l( heta) = argunderset{ heta}{max}\, heta^8(1- heta)^2 ]

其中，(l( heta))为观测变量序列的似然函数（likelihood function of the observation sequence）。对(l( heta))求偏导

[frac{partial l( heta)}{partial heta} = heta^7(1- heta)(8-10 heta) Rightarrow hat{ heta} = 0.8 ]

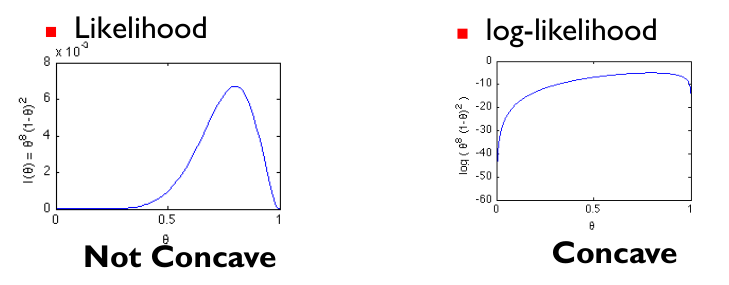
因为似然函数(l( heta))不是凹函数（concave），求解极大值困难。一般地，使用与之具有相同单调性的log-likelihood，如图所示

凹函数（concave）与凸函数（convex）的定义如图所示：

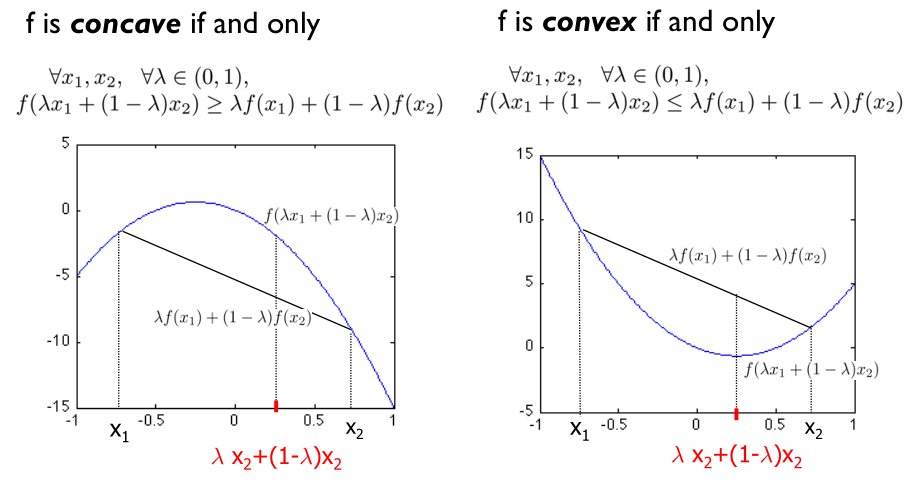
从图中可以看出，凹函数“容易”求解极大值，凸函数“容易”求解极小值。

2. EM算法

EM算法（Expectation Maximization）是在含有隐变量（latent variable）的模型下计算最大似然的一种算法。所谓隐变量，是指我们没有办法观测到的变量。比如，有两枚硬币A、B，每一次随机取一枚进行抛掷，我们只能观测到硬币的正面与反面，而不能观测到每一次取的硬币是否为A；则称每一次的选择抛掷硬币为隐变量。

用Y表示观测数据，Z表示隐变量；Y和Z连在一起称为完全数据( complete-data )，观测数据Y又称为不完全数据(incomplete-data)。观测数据的似然函数：

[P(Y | heta) = sum_{Z} P(Z| heta)P(Y|Z, heta) ]

求模型参数的极大似然估计：

[hat{ heta} = argunderset{ heta}{max}\, log P(Y | heta) ]

因为含有隐变量，此问题无法求解。因此，Dempster等人提出EM算法用于迭代求解近似解。EM算法比较简单，分为两个步骤：

• E步（E-step），以当前参数( heta^{(i)})计算(Z)的期望值

[Q( heta, heta^{(i)}) = mathbb{E}_Z[log P(Y,X| heta)| Y, heta^{(i)}] ]

• M步（M-step），求使(Q( heta, heta^{(i)}))极大化的( heta)，确定第(i+1)次迭代的参数的估计值( heta^{(i+1)})

[ heta^{(i+1)} = argunderset{ heta}{max}\, Q( heta, heta^{(i)}) ]

如此迭代直至算法收敛。关于算法的推导及收敛性证明，可参看李航的《统计学习方法》及Andrew Ng的《CS229 Lecture notes》。这里有一些极大似然以及EM算法的生动例子。

3. 实例

[2]中给出极大似然与EM算法的实例。如图所示，有两枚硬币A、B，每一个实验随机取一枚抛掷10次，共5个实验，我们可以观测到每一次所取的硬币，估计参数A、B为正面的概率( heta = ( heta_A, heta_B))，根据极大似然估计求解

如果我们不能观测到每一次所取的硬币，只能用EM算法估计模型参数，算法流程如图所示：

隐变量(Z)为每次实验中选择A或B的概率，则第一个实验选择A的概率为

[P(z_1 = A |y_1, heta^{(0)}) = frac{P(z_1 = A |y_1, heta^{(0)})}{P(z_1 = A |y_1, heta^{(0)}) + P(z_1 = B |y_1, heta^{(0)})} = frac{0.6^5*0.4^5}{0.6^5*0.4^5 + 0.5^{10}} = 0.45 ]

按照上面的计算方法可依次求出隐变量(Z)，然后计算极大化的( heta^{(i)})。经过10次迭代，最终收敛。

4. 参考资料

[1] 李航，《统计学习方法》.
[2] Chuong B Do & Serafim Batzoglou, What is the expectation maximization algorithm?
[3] Pieter Abbeel, Maximum Likelihood (ML), Expectation Maximization (EM).
[4] Rudan Chen,【机器学习算法系列之一】EM算法实例分析.