Given a binary tree, we install cameras on the nodes of the tree.
Each camera at a node can monitor its parent, itself, and its immediate children.
Calculate the minimum number of cameras needed to monitor all nodes of the tree.
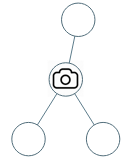
Example 1:
Input: [0,0,null,0,0]
Output: 1
Explanation: One camera is enough to monitor all nodes if placed as shown.
Example 2:
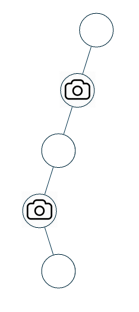
Input: [0,0,null,0,null,0,null,null,0]
Output: 2
Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
Note:
- The number of nodes in the given tree will be in the range
[1, 1000]. - Every node has value 0.
做了很久,还是写不出来,看了网上的答案。确实很精妙。利用了返回值表达了三种状态,利用引用存储最后结果。
还有一点就是在放相机的时候,在递归函数里,父节点一定比节点有优势,能放父节点一定放父节点,拿叶节点来
举例,此时如果放叶节点,能影响到的点只有它本身和父节点,而父节点能影响到子节点,本身,和它的父节点。
所以这是一个贪心算法。
class Solution {
public:
int minCameraCover(TreeNode* root) {
int sum=0;
if(dfs(root,sum)==0) sum++;// if root is not monitored, we place an additional camera here
return sum;
}
int dfs(TreeNode * tr, int& sum){
if(!tr) return 1;
int l=dfs(tr->left,sum), r=dfs(tr->right,sum);
if(l==0||r==0){// if at least 1 child is not monitored, we need to place a camera at current node
sum++;
return 2;
}else if(l==2||r==2){// if at least 1 child has camera, the current node if monitored. Thus, we don't need to place a camera here
return 1;
}else{// if both children are monitored but have no camera, we don't need to place a camera here. We place the camera at its parent node at the higher level.
return 0;
}
return -1;// this return statement won't be triggered
}
};