机器学习【四】决策树

决策树原理

对一系列问题进行if/else推导，最终实现决策

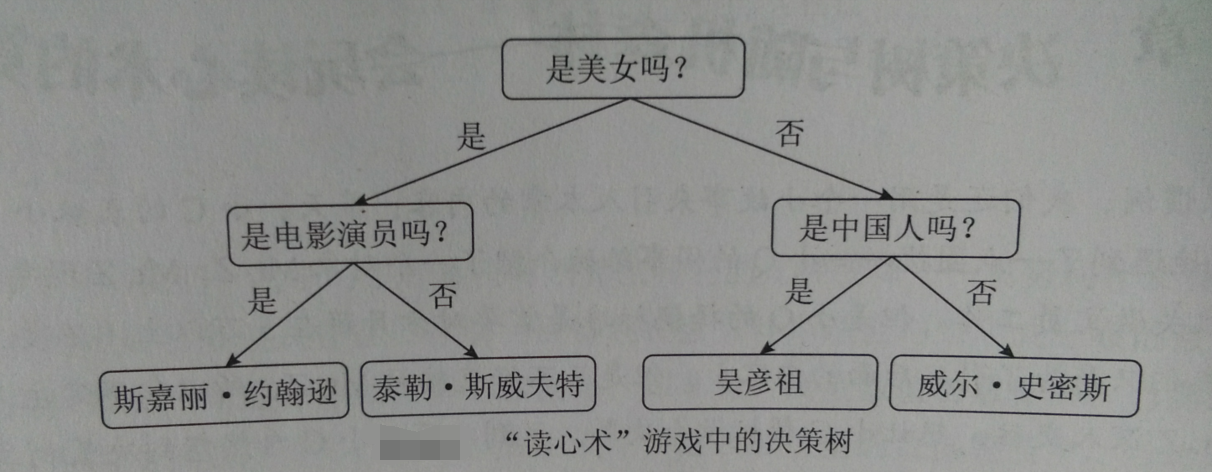
决策树构建

#导入numpy
import numpy as np
#导入画图工具
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
#导入树模型和数据集加载工具
from sklearn import tree,datasets
#导入数据集拆分工具
from sklearn.model_selection import train_test_split
wine = datasets.load_wine()
#只选数据集前两个特征
X = wine.data[:,:2]
y = wine.target
#将数据集拆分为训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X,y)

用决策树分类器分类【为了便于图形演示，仍然只选取数据集样本中的前两个特征】

#设定决策树分类器最大深度为1
clf = tree.DecisionTreeClassifier(max_depth=1)
#拟合训练集数据
clf.fit(X_train,y_train)

【结果分析】：Jupyter Notebook 把分类器的参数返回。max_depth参数，是决策树深度

分类器表现，用图形画出来

#定义图像中分区的颜色和散点图
cmap_light = ListedColormap(['#FFAAAA','#AAFFAA','#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF'])
#用样本的两个特征值创建图像和横轴和纵轴
x_min,x_max =  X[:,0].min() -1,X[:,0].max() +1
y_min,y_max =  X[:,1].min() -1,X[:,1].max() +1
#用不同的背景色表示不同的分类
xx,yy = np.meshgrid(np.arange(x_min,x_max,.02),np.arange(y_min,y_max,.02))
z = clf.predict(np.c_[(xx.ravel(),yy.ravel())])
#将每个分类中的样本分配不同的颜色
z = z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx,yy,z,cmap=cmap_light)
#用散点图把样本表示出来
plt.scatter(X[:,0],X[:,1],c=y,cmap=cmap_bold,edgecolor='k',s=20)
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title("Classifier:(max_depth= 1 )")
plt.show()

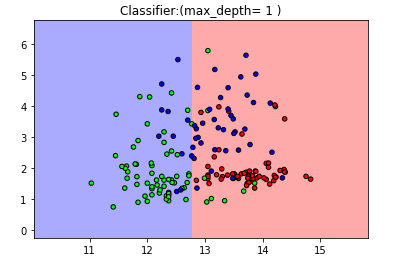
【显然，分类器表现不太好，只分为2类】

加大深度

#设定决策树最大深度为3
clf2 = tree.DecisionTreeClassifier(max_depth = 3)
#重新拟合数据
clf2.fit(X_train,y_train)

 让max_depth=3

#定义图像中分区的颜色和散点图
cmap_light = ListedColormap(['#FFAAAA','#AAFFAA','#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF'])
#用样本的两个特征值创建图像和横轴和纵轴
x_min,x_max =  X[:,0].min() -1,X[:,0].max() +1
y_min,y_max =  X[:,1].min() -1,X[:,1].max() +1
#用不同的背景色表示不同的分类
xx,yy = np.meshgrid(np.arange(x_min,x_max,.02),np.arange(y_min,y_max,.02))
z = clf2.predict(np.c_[(xx.ravel(),yy.ravel())])
#将每个分类中的样本分配不同的颜色
z = z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx,yy,z,cmap=cmap_light)
#用散点图把样本表示出来
plt.scatter(X[:,0],X[:,1],c=y,cmap=cmap_bold,edgecolor='k',s=20)
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title("Classifier:(max_depth= 3 )")
plt.show()

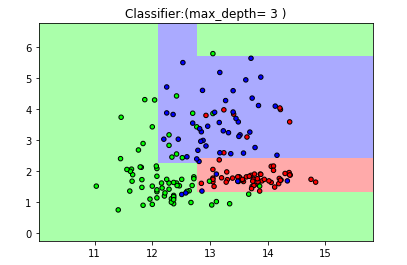
 【结果分析】：最大深度为3时，大部分分类正确

设置max_depth = 5,继续绘图：

#设定决策树最大深度为5
clf3 = tree.DecisionTreeClassifier(max_depth = 5)
#重新拟合数据
clf3.fit(X_train,y_train)

#定义图像中分区的颜色和散点图
cmap_light = ListedColormap(['#FFAAAA','#AAFFAA','#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF'])
#用样本的两个特征值创建图像和横轴和纵轴
x_min,x_max =  X[:,0].min() -1,X[:,0].max() +1
y_min,y_max =  X[:,1].min() -1,X[:,1].max() +1
#用不同的背景色表示不同的分类
xx,yy = np.meshgrid(np.arange(x_min,x_max,.02),np.arange(y_min,y_max,.02))
z = clf3.predict(np.c_[(xx.ravel(),yy.ravel())])
#将每个分类中的样本分配不同的颜色
z = z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx,yy,z,cmap=cmap_light)
#用散点图把样本表示出来
plt.scatter(X[:,0],X[:,1],c=y,cmap=cmap_bold,edgecolor='k',s=20)
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title("Classifier:(max_depth= 5 )")
plt.show()

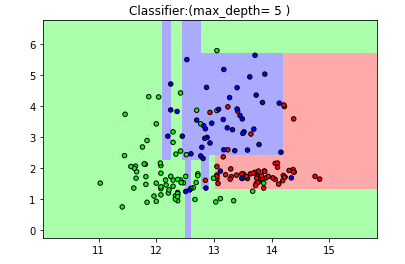
用graphviz库展示决策树在每一层干嘛的过程：【演示决策树的工作流程，不必要安装】

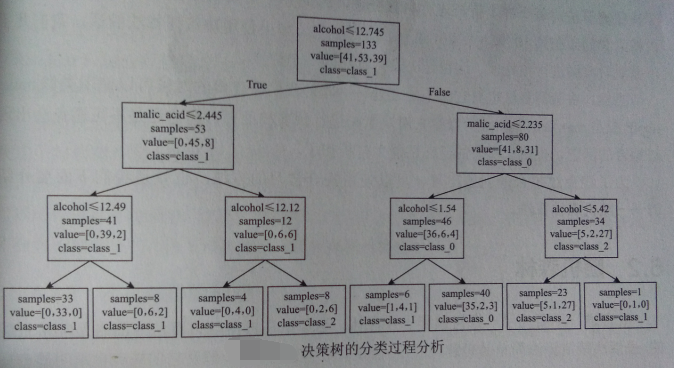
 决策树的优缺点

优点

• 很容易将模型可视化
• 由于决策树算法对每个样本特征单独处理——> 不需要对数据进行转换
• 不需要对数据预处理

缺点

• 即使有预剪枝处理【使用max_depth、max_leaf_nodes参数】，还是不可避免出现过拟合问题
• 泛化性能大打折扣

为了避免过拟合——> 使用集合学习——> 随机森林算法