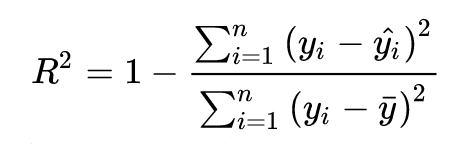Sklearn线性回归
原理
线性回归是最为简单而经典的回归模型,用了最小二乘法的思想,用一个n-1维的超平面拟合n维数据
数学形式
[y(w,x)=w_0+w_1x_1+w_2x_2+…+w_nx_n
]
其中称(w=(w_1,w_2,w_3,...w_n))为系数矩阵(coef_),称(w_0)为截距(intercept_)
基本步骤
- 准备数据集
- 使用线性回归
- 训练模型
- 使用训练后的模型预测
- 模型评估
下面以二维数据举例
例子
#coding=utf-8
import pandas as pd
from sklearn import linear_model
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
def main():
#数据预处理
ad = pd.read_csv('./Advertising.csv',index_col=0)
#为了方便,只取一列作为研究
X = ad[['TV']] #注意此时X的数据类型是dataFrame,如果只有一个括号,类型为Series会报错
Y = ad[['Sales']]
#这里采用交叉验证法划分数据集
X_train, X_test, Y_train, Y_test =train_test_split(X, Y)
#创建回归模型对象
lr = linear_model.LinearRegression()
lr.fit(X_train.values.reshape(-1, 1), Y_train.values.reshape(-1, 1))
#显示训练结果
print lr.intercept_,lr.coef_
print lr.score(X_test, Y_test) #用R^2评估
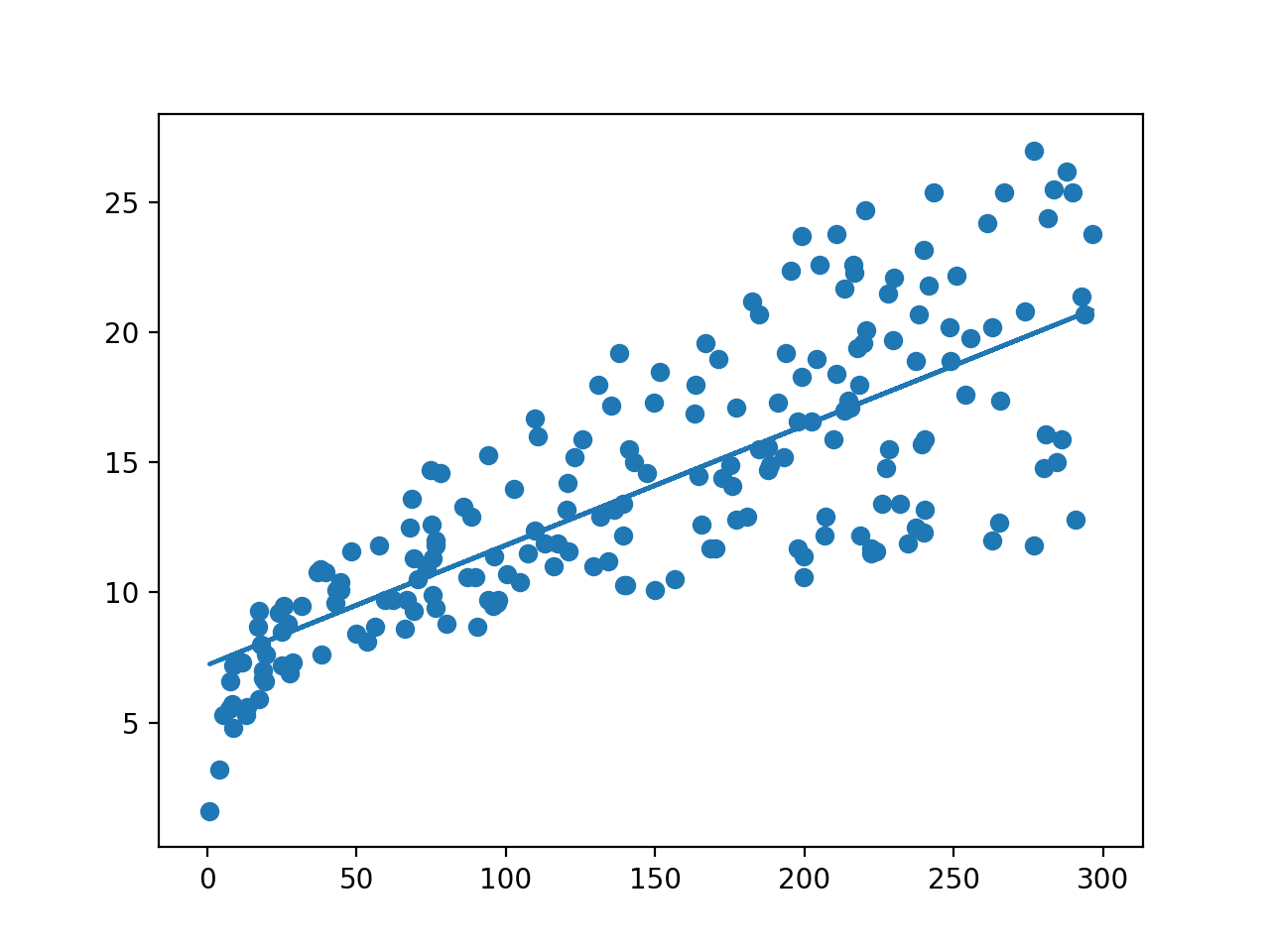
plt.plot(X,lr.predict(X))
plt.scatter(X,Y)
plt.show()
if __name__ == '__main__':
main()
'''
输出结果
[ 7.21071682] [[ 0.0460963]]
0.713025893451
'''
关于模型评估
这里采用的是(R^2)拟合优度检验,是一个属于0~1的值,(R^2)越大表示拟合程度越好