sklearn逻辑回归
logistics回归名字虽然叫回归,但实际是用回归方法解决分类的问题,其形式简洁明了,训练的模型参数还有实际的解释意义,因此在机器学习中非常常见。
理论部分
设数据集有n个独立的特征x,与线性回归的思路一样,先得出一个回归多项式:
[y(x) = w_0+w_1x_1+w_2x_2+…+w_nx_n
]
但这个函数的值域是([-infty,+infty]),如果使用符号函数进行分类的话曲线又存在不连续的问题。这个时候,就要有请我们的sigmoid函数登场了,其定义如下:
[f(x)=frac{1}{1+e^{-x}}
]
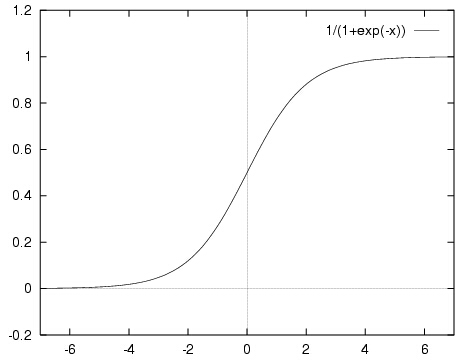
这个函数属于([0,1]),而且连续可导,如果把纵坐标看成概率,那么就可以根据某个对象属于某一类的概率来进行分类了。
顺着这样的思路,我们定义几率比(odds ratio):
[y(x)=ln(frac{p(x)}{1-p(x)})
]
这里(p(x))表示该属性组合x属于第一类(正类)的概率,对应的(1-p(x))表示该属性组合x属于第二类(反类)的概率。可以解得:
[p(x)=frac{1}{1+e^{-(w_0+w_1x_1+w_2x_2+…+w_nx_n)}}
]
如果模型已经训练好,我们就可以根据w和x来求出(p(x)),如果(p(x)>0.5)就判断为正类,否则判断为反类。
之后就是训练参数的问题,可以采用极大似然估计的方法估算权重。
理论部分差不多就结束了,值得注意的是,训练出的参数(w_i)不光可以分类,还具有实际意义,它表示属性(x_i)对于总体对象属于哪一类的影响程度。因此逻辑回归虽然形式简单,但解释力比较强。
sklearn代码实现
#coding=utf-8
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn import linear_model
import numpy as np
def main():
iris = datasets.load_iris() #典型分类数据模型
#这里我们数据统一用pandas处理
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data['class'] = iris.target
#这里只取两类,class=0或1
data = data[data['class']!=2]
#为了可视化方便,这里取两个属性为例
X = data[['sepal length (cm)','sepal width (cm)']]
Y = data[['class']]
#划分数据集
X_train, X_test, Y_train, Y_test =train_test_split(X, Y)
#创建回归模型对象
lr = linear_model.LogisticRegression()
lr.fit(X_train, Y_train)
#显示训练结果
print lr.coef_, lr.intercept_
print lr.score(X_test, Y_test) #score是指分类的正确率
#作图2x1
plt.subplot(211)
#区域划分
h = 0.02
x_min, x_max = X.iloc[:, 0].min() - 1, X.iloc[:, 0].max() + 1
y_min, y_max = X.iloc[:, 1].min() - 1, X.iloc[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
#做出原来的散点图
class1_x = X.loc[Y['class']==0,'sepal length (cm)']
class1_y = X.loc[Y['class']==0,'sepal width (cm)']
l1 = plt.scatter(class1_x,class1_y,color='b',label=iris.target_names[0])
class1_x = X.loc[Y['class']==1,'sepal length (cm)']
class1_y = X.loc[Y['class']==1,'sepal width (cm)']
l2 = plt.scatter(class1_x,class1_y,color='r',label=iris.target_names[1])
plt.legend(handles = [l1, l2], loc = 'best')
#做出概率分布图sigmoid
plt.subplot(212)
x0 = np.linspace(-5, 5, 200)
#与lr.predict_proba(X)[:,1]等价
plt.plot(x0,1/(1+np.exp(-x0)),linestyle = "-.",color='k')
x1 = np.dot(X[data['class']==0],lr.coef_.T)+lr.intercept_
l3 = plt.scatter(x1,1/(1+np.exp(-x1)),color='b',label=iris.target_names[0])
x2 = np.dot(X[data['class']==1],lr.coef_.T)+lr.intercept_
l4 = plt.scatter(x2,1/(1+np.exp(-x2)),color='r',label=iris.target_names[1])
plt.legend(handles = [l3, l4], loc = 'best')
plt.grid(True)
plt.show()
if __name__ == '__main__':
main()
测试结果
[[ 1.9809081 -3.2648774]] [-0.60409876]
1.0
