P2048 [NOI2010]超级钢琴

题目描述

小Z是一个小有名气的钢琴家，最近C博士送给了小Z一架超级钢琴，小Z希望能够用这架钢琴创作出世界上最美妙的音乐。

这架超级钢琴可以弹奏出n个音符，编号为1至n。第i个音符的美妙度为Ai，其中Ai可正可负。

一个“超级和弦”由若干个编号连续的音符组成，包含的音符个数不少于L且不多于R。我们定义超级和弦的美妙度为其包含的所有音符的美妙度之和。两个超级和弦被认为是相同的，当且仅当这两个超级和弦所包含的音符集合是相同的。

小Z决定创作一首由k个超级和弦组成的乐曲，为了使得乐曲更加动听，小Z要求该乐曲由k个不同的超级和弦组成。我们定义一首乐曲的美妙度为其所包含的所有超级和弦的美妙度之和。小Z想知道他能够创作出来的乐曲美妙度最大值是多少。

输入输出格式

输入格式：

输入第一行包含四个正整数n, k, L, R。其中n为音符的个数，k为乐曲所包含的超级和弦个数，L和R分别是超级和弦所包含音符个数的下限和上限。

接下来n行，每行包含一个整数Ai，表示按编号从小到大每个音符的美妙度。

输出格式：

输出只有一个整数，表示乐曲美妙度的最大值。

输入输出样例

输入样例#1： 

4 3 2 3
3
2
-6
8

输出样例#1： 

11

说明

共有5种不同的超级和弦：

1.    音符1 ~ 2，美妙度为3 + 2 = 5
2.    音符2 ~ 3，美妙度为2 + (-6) = -4
3.    音符3 ~ 4，美妙度为(-6) + 8 = 2
4.    音符1 ~ 3，美妙度为3 + 2 + (-6) = -1
5.    音符2 ~ 4，美妙度为2 + (-6) + 8 = 4

最优方案为：乐曲由和弦1，和弦3，和弦5组成，美妙度为5 + 2 + 4 = 11。

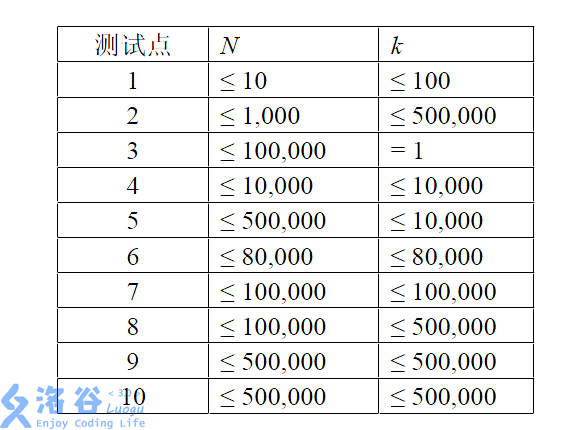
所有数据满足：-1000 ≤ Ai ≤ 1000，1 ≤ L ≤ R ≤ n且保证一定存在满足要求的乐曲。

Solution：

　　考试时写挂，只会暴力20分+单调队列10分。

　　然后正解非常有意思，可以类比序列合并那道题。

　　首先，很显然每次一个个累加是行不通的，肯定得用到前缀和。其次，对于位置$i$，以它为左端点的一个合法区间$[i,j],jin[min(i+L-1,n),min(i+R-1,n)]$，很显然我们要最大化$s[j]$以便$s[j]-s[i-1]$最大。由于最大值不变，我们可以倍增预处理保存一下一段区间最大值的下标。

　　然后我们由序列合并的思路，不难想到用堆去维护所有合法答案中的前$k$大的值。

　　那么具体实现我们可以设$g(l,r,x,y)$表示的是所求最值的区间限制范围为$[l,r]$，左节点为$x$，右节点$y,yin[l,r]$且$s[y]$为该段区间的最大值，那么我们把$g(l,r,x,y)$放入堆中（最开始$l=min(i+L-1,n),r=min(i+R-1,n)$）。每当$pop$出一个$g(l,r,x,y)$，先累加答案，然后显然当$l!=y$时$[l,y-1]$这段区间中可能存在次优解，同理还有当$r!=y$时$[y+1,r]$也有可能存在次优解，所以还得把这两段区间的$g$放入堆中。$g$实现时写个结构体和构造函数就好了。

　　时间复杂度为$O(k log n)$，就能过了。

代码：

#include<bits/stdc++.h>
#define il inline
#define ll long long
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=500005,M=20;
ll s[N],f[N][M],ans;
int n,k,L,R;

il int gi(){
    int a=0;char x=getchar();bool f=0;
    while((x<'0'||x>'9')&&x!='-')x=getchar();
    if(x=='-')x=getchar(),f=1;
    while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar();
    return f?-a:a;
}

il void pre(){
    For(i,1,n) f[i][0]=i;
    for(int j=1;(1<<j)<=n;j++) for(int i=1;i+(1<<j)-1<=n;i++){
        int x=f[i][j-1],y=f[i+(1<<(j-1))][j-1];
        f[i][j]=s[x]>s[y]?x:y;
    }
}

il int query(int l,int r){
    int k=log2(r-l+1);
    int x=f[l][k],y=f[r-(1<<k)+1][k];
    return s[x]>s[y]?x:y;
}

struct node{
    int l,r,L,R;
    node(int c,int a,int b){l=a,r=b,L=c,R=query(l,r);}
    bool operator<(const node &a)const {return s[R]-s[L-1]<s[a.R]-s[a.L-1];}
};
priority_queue<node>q;

il void solve(){
    n=gi(),k=gi(),L=gi(),R=gi();
    For(i,1,n) s[i]=gi()+s[i-1];
    pre();
    For(i,1,n) if(i+L-1<=n) q.push(node(i,i+L-1,min(i+R-1,n)));
    while(k--){
        int x=q.top().L,y=q.top().R,l=q.top().l,r=q.top().r;q.pop();
        ans+=s[y]-s[x-1];
        if(l!=y) q.push(node(x,l,y-1));
        if(r!=y) q.push(node(x,y+1,r));
    }
    cout<<ans;
}

int main(){
    solve();
    return 0;
}