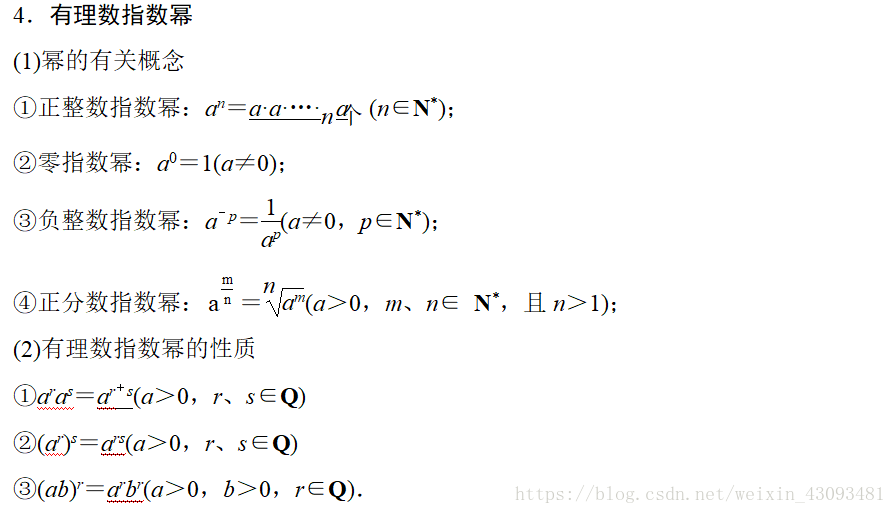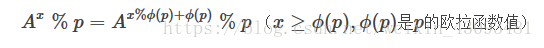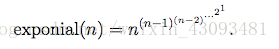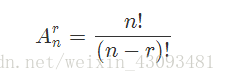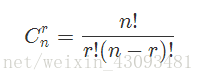ACM常用模板数论

常用数论模板，代码大多数来自网络，个人整理总结，不定期更新

基本函数及其性质：

---

最大公约数与最小公倍数：

gcd：                       //最大公约数
    int gcd(int a,int b)
    {
        if(b==0)  return a;
        else return gcd(b,a%b);
    }

lcm:                  //最小公倍数
    int lcm(int a,int b)
   {
        return a/gcd(a,b)*b;    //防止溢出
    }

快速幂：

a,n,p都在long long 以内

LL pow(LL a, LL n, LL p)    //快速幂 a^n % p
{
    LL ans = 1;
    while(n)
    {
        if(n & 1) ans = ans * a % p;          //若不取模就去掉p
        a = a * a % p;
        n >>= 1;
    }
    return ans;
}

n超过long long

typedef unsigned long long LL;
string str;
int input[10000005];
int output[10000005];
int len;
int sum=1,d=0,k=0;
void to_bin(string str)               //将大整数转换为二进制，转换后为逆序
{
    len=str.size();
    for(int i=0;i<len;i++)
        input[i]=str[i]-'0';
    memset(output,0,sizeof(output));
    sum=1,d=0,k=0;
    while(sum)
    {
        sum = 0;
        for(int i=0;i<len;i++){
            d = input[i] / 2;
            sum += d;
            if(i == (len - 1)){
                output[k++] = input[i] % 2;
            }
            else
                input[i+1] += (input[i]%2)*10;
            input[i] = d;
        }
    }
}
LL pow(LL a, int n[], LL p)    //快速幂 a^n % p
{
    LL ans = 1;
    int i=0;
    while(i<k)
    {
        if(n[i] == 1) ans = ans * a % p;
        a = a * a % p;
        i++;
    }
    return ans;
}
int main()
{
    LL a,b,c;
    while(cin>>a>>str>>c)
    {
        to_bin(str);
        cout<<pow(a,output,c)<<endl;
    }
}

素数筛：

埃氏素数筛：

vector<int>prime;        //其中存储2-n的所有素数
bool is_prime[MAXN]   //存储第i项是否为素数 
void find_prime(int n)
{
    int p=0;
    for(int i=2;i<=n;i++)
        is_prime[i]=true;
    is_prime[0]=is_prime[1]=false;
    for(int i=2;i<=n;i++)
    {
        if(is_prime[i])
        {
            prime.push_back(i);
            for(int j=2*i;j<=n;j+=i)
                is_prime[j]=false;
        }
    }
}

线性素数筛：

#include <cstdio>
#include <bitset>
using namespace std;
bitset<10000010> g;
int n,m,x,p[1000010],top=0;
int main()
{
    scanf("%d%d",&n,&m);
    g[0]=1;    g[1]=1;
    for(int i=2;i<=n;++i)
    {
        if(g[i]==0)
            p[++top]=i;
        for(int j=1;j<=top&&p[j]*i<=n;++j)
        {
            g[i*p[j]]=1;
            if(i%p[j]==0)
                break;
        }
    }
    for(int i=1;i<=m;++i)
    {
        scanf("%d",&x);
        if(g[x])
            printf("No\n");
        else
            printf("Yes\n");
    }
    return 0;
}

素性测试：

miller_rabin：

概率算法，能处理10^19范围数

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<time.h>
#include<iostream>
#include<algorithm>
using namespace std;
//****************************************************************
// Miller_Rabin 算法进行素数测试
//速度快，而且可以判断 <2^63的数
//****************************************************************
const int S=20;//随机算法判定次数，S越大，判错概率越小
//计算 (a*b)%c.   a,b都是long long的数，直接相乘可能溢出的
//  a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
    a%=c;
    b%=c;
    long long ret=0;
    while(b)
    {
        if(b&1){ret+=a;ret%=c;}
        a<<=1;
        if(a>=c)a%=c;
        b>>=1;
    }
    return ret;
}
//计算  x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
    if(n==1)return x%mod;
    x%=mod;
    long long tmp=x;
    long long ret=1;
    while(n)
    {
        if(n&1) ret=mult_mod(ret,tmp,mod);
        tmp=mult_mod(tmp,tmp,mod);
        n>>=1;
    }
    return ret;
}
//以a为基,n-1=x*2^t      a^(n-1)=1(mod n)  验证n是不是合数
//一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
    long long ret=pow_mod(a,x,n);
    long long last=ret;
    for(int i=1;i<=t;i++)
    {
        ret=mult_mod(ret,ret,n);
        if(ret==1&&last!=1&&last!=n-1) return true;//合数
        last=ret;
    }
    if(ret!=1) return true;
    return false;
}
// Miller_Rabin()算法素数判定
//是素数返回true.(可能是伪素数，但概率极小)
//合数返回false;
bool Miller_Rabin(long long n)
{
    if(n<2)return false;
    if(n==2)return true;
    if((n&1)==0) return false;//偶数
    long long x=n-1;
    long long t=0;
    while((x&1)==0){x>>=1;t++;}
    for(int i=0;i<S;i++)
    {
        long long a=rand()%(n-1)+1;//rand()需要stdlib.h头文件
        if(check(a,n,x,t))
            return false;//合数
    }
    return true;
}
//************************************************
//pollard_rho 算法进行质因数分解
//************************************************
long long factor[100];//质因数分解结果（刚返回时是无序的）
int tol;//质因数的个数。数组小标从0开始
long long gcd(long long a,long long b)
{
    if(a==0)return 1;//???????
    if(a<0) return gcd(-a,b);
    while(b)
    {
        long long t=a%b;
        a=b;
        b=t;
    }
    return a;
}
long long Pollard_rho(long long x,long long c)
{
    long long i=1,k=2;
    long long x0=rand()%x;
    long long y=x0;
    while(1)
    {
        i++;
        x0=(mult_mod(x0,x0,x)+c)%x;
        long long d=gcd(y-x0,x);
        if(d!=1&&d!=x) return d;
        if(y==x0) return x;
        if(i==k){y=x0;k+=k;}
    }
}
//对n进行素因子分解
void findfac(long long n)
{
    if(Miller_Rabin(n))//素数
    {
        factor[tol++]=n;
        return;
    }
    long long p=n;
    while(p>=n)p=Pollard_rho(p,rand()%(n-1)+1);
    findfac(p);
    findfac(n/p);
}
int main()
{
    //srand(time(NULL));//需要time.h头文件//POJ上G++不能加这句话
    long long n;
    while(scanf("%I64d",&n)!=EOF)
    {
        tol=0;
        findfac(n);
        for(int i=0;i<tol;i++)printf("%I64d ",factor[i]);
        printf("\n");
        if(Miller_Rabin(n))printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

逆序数：

#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int N=100050;
int n;
long long c[N];      //c[n]表示a[1~n]的和，a数组省略
struct node
{
    int val,pos;
}a[100005];
int lowbit(int x)       //求2^k
{
    return x & -x;
}
long long getsum(int n)   //区间查询，求a[1~n]的和
{
    long long res = 0;
    while(n>0)
    {
        res+=c[n];
        n=n-lowbit(n);
    }
    return res;
}
int change(int x)  //单点更新，将c[x]的值加1
{
     while(x<=n)
     {
         c[x]++;
         x+=lowbit(x);
     }
}
bool cmp(node a,node b)         //包含相同数
{
    if(a.val!=b.val)
        return a.val>b.val;
    return a.pos>b.pos;
}
int main()
{
    std::ios::sync_with_stdio(false);
    while(cin>>n)
    {
        memset(c,0,sizeof(c));
        for(int i=1;i<=n;i++)
        {
            cin>>a[i].val;
            a[i].pos=i;
        }
        sort(a+1,a+n+1,cmp);
        long long cnt=0;
        for(int i=1;i<=n;i++)
        {
            change(a[i].pos);                     //修改最大数位置的值
            cnt+=getsum(a[i].pos-1);     //最大数位置之前的所有位置和，即区间求和，可知比当前数小的数有多少个
        }
        cout<<cnt<<endl;
    }
    return 0;
}

欧拉函数：

定义： 在数论中，对正整数n，欧拉函数是小于等于n的数中与n互质的数的数目。并且用符号φ(n)表示一个整数的欧拉函数。
性质：
1.对于质数p， φ(p) = p - 1。注意φ(1)=1
2. 欧拉定理：对于互质的正整数a和n，有aφ(n) ≡ 1 mod n。
3. 若m,n互质，φ(mn)=φ(m)φ(n)
4. 当n为奇数时，φ(2n)=φ(n)
5.当n大于2时，所有φ(n)都是偶数
6.当n大于6时，所有φ(n)都是合数

朴素方式O(sqrt(n))：

//直接求解欧拉函数  
  int euler(int n){ //返回euler(n)   
       int res=n,a=n;  
       for(int i=2;i*i<=a;i++){  
           if(a%i==0){  
               res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出   
               while(a%i==0) a/=i;  
           }  
       }  
      if(a>1) res=res/a*(a-1);  
      return res;  
}

线性筛法O(Nlog(m))：

void Init(){     
     euler[1]=1;    
     for(int i=2;i<Max;i++)    
       euler[i]=i;    
     for(int i=2;i<Max;i++)    
        if(euler[i]==i)    
           for(int j=i;j<Max;j+=i)    
              euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出
}

---

指数降幂公式：

计算exponial（n）：

#include <iostream>
using namespace std;

typedef long long ll;  
ll n,m,ans;

ll euler(ll n){ //返回euler(n) ，计算欧拉函数值
     ll res=n,a=n;  
     for(ll i=2;i*i<=a;i++){  
         if(a%i==0){  
             res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出   
             while(a%i==0) a/=i;  
         }  
     }  
     if(a>1) res=res/a*(a-1);  
     return res;  
}
ll fast_mod(ll x,ll n,ll Max)  //快速幂
{  
    ll res=1;  
    while(n>0)  
    {  
        if(n & 1)  
            res=(res*x)%Max;  
        x=(x*x)%Max;  
        n >>= 1;  
    }  
    return res;  
}
ll func(ll n,ll m){      //循环求解

    if(m==1) return 0;

    if(n<=5){
        ll ans=1;
        for(int i=1;i<=n;i++){
            ans=fast_mod(i,ans,m);
        }
        return ans;
    }else{
        ll phi=euler(m);
        ll z=func(n-1,phi);
        ans=fast_mod(n,phi+z,m);
    }
    return ans;

}
void solve(){        //计算exponial（n）
    scanf("%lld%lld",&n,&m);
    printf("%lld\n",func(n,m));
}
int main(){
    solve();

    return 0;
}

---

组合计数：

排列数：

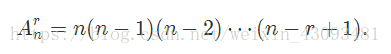
若n和r都是整数，且0<=r<=n,有

---

不尽相异元素全排列：

---

组合数：

重复组合数：

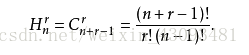
二项式定理：

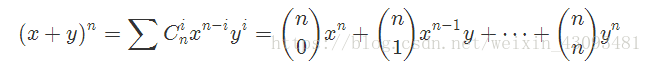
常见恒等式：

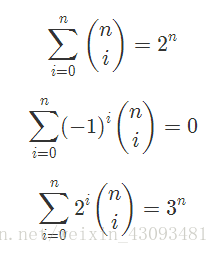
帕斯卡恒等式：

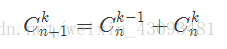
容斥原理：

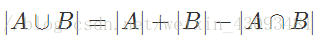
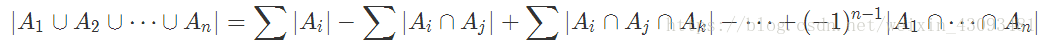
组合数取模：

typedef long long LL;
const LL maxn(1000005), mod(1e9 + 7);
LL Jc[maxn];
void calJc()    //求maxn以内的数的阶乘
{
    Jc[0] = Jc[1] = 1;
    for(LL i = 2; i < maxn; i++)
        Jc[i] = Jc[i - 1] * i % mod;
}
/*
//拓展欧几里得算法求逆元
void exgcd(LL a, LL b, LL &x, LL &y)    //拓展欧几里得算法
{
    if(!b) x = 1, y = 0;
    else
    {
        exgcd(b, a % b, y, x);
        y -= x * (a / b);
    }
}
LL niYuan(LL a, LL b)   //求a对b取模的逆元
{
    LL x, y;
    exgcd(a, b, x, y);
    return (x + b) % b;
}
*/
//费马小定理求逆元
LL pow(LL a, LL n, LL p)    //快速幂 a^n % p
{
    LL ans = 1;
    while(n)
    {
        if(n & 1) ans = ans * a % p;
        a = a * a % p;
        n >>= 1;
    }
    return ans;
}
LL niYuan(LL a, LL b)   //费马小定理求逆元
{
    return pow(a, b - 2, b);
}
LL C(LL a, LL b)    //计算C(a, b)
{
    return Jc[a] * niYuan(Jc[b], mod) % mod
        * niYuan(Jc[a - b], mod) % mod;
}

---

母函数：

http://www.wutianqi.com/?p=596
用于计算组合问题可能情况数

普通母函数：

普通母函数通常解决类似如下的问题： 给5张1元，4张2元，3张5元，要得到15元，有多少种组合？ 某些时候会规定至少使用3张1元、1张2元、0张5元。 某些时候会规定有无数张1元、2元、5元。

const int MAX=10000;
const int INF=0x3f3f3f3f;
//为计算结果，b为中间结果。
// K对应具体问题中物品的种类数。
//v[i]表示该乘积表达式第i个因子的权重，对应于具体问题的每个物品的价值或者权重。
//n1[i]表示该乘积表达式第i个因子的起始系数，对应于具体问题中的每个物品的最少个数，即最少要取多少个。0
//n2[i]表示该乘积表达式第i个因子的终止系数，对应于具体问题中的每个物品的最多个数，即最多要取多少个。INF
//P为可能出现的最大指数(所求情况)
int a[MAX],b[MAX],P;
int k,v[MAX],n1[MAX],n2[MAX];
//初始化a
void cal(int n)       //n为种类数
{
    memset(a,0,sizeof(a));
    a[0]=1;
    for (int i=1;i<=n;i++)//循环每个因子
    {
        memset(b,0,sizeof(b));
        for (int j=n1[i];j<=n2[i]&&j*v[i]<=P;j++)//循环每个因子的每一项
            for (int k=0;k+j*v[i]<=P;k++)//循环a的每个项
                b[k+j*v[i]]+=a[k];//把结果加到对应位
        memcpy(a,b,sizeof(b));//b赋值给a
    }
}

指数母函数：

用于求多重排列数
如以下问题： 假设有8个元素，其中a1重复3次，a2重复2次，a3重复3次。从中取r个排列，求其排列数。 对于上面的问题“假设有8个元素，其中a1重复3次，a2重复2次，a3重复3次。从中取r个排列，求其排列数。

double c1[N],c2[N];
LL fac[N];
void Fac()            //求阶乘
{
    fac[0]=1;
    for(int i=1;i<=N;i++)
        fac[i]=fac[i-1]*i;
}

int a[N];           //1~n每种的个数
void cal(int n,int m)          //有n种，取m个
{
    memset(c1,0,sizeof(c1));
    memset(c2,0,sizeof(c2));

    c1[0]=1.0/fac[0];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
            for(int k=0;k+j<=m && k<=a[i];k++)
                c2[k+j]+=c1[j]/fac[k];
        for(int j=0;j<=m;j++)
            c1[j]=c2[j],c2[j]=0;
    }
}
ans=c1[m]*fac[m];           //取m个时的多重排列数

Polya计数：

定义：设G是有限集X上的置换群，点a,b∈X称为”等价”的，当且仅当，存在π∈G使得π(a)=b，记为a~b，这种等价条件下，X的元素形成的等价类称为G的轨道，它是集X的一个子集，G的任意两个不同的轨道之交是空集，所以置换群G的轨道全体是集合X的一个划分，构成若干个等价类，等价类的个数记为L。
Zk (K不动置换类)：设G是1…n的置换群。若K是1…n中某个元素，G中使K保持不变的置换的全体，记以Zk，叫做G中使K保持不动的置换类，简称K不动置换类。
Ek(等价类)：设G是1…n的置换群。若K是1…n中某个元素，K在G作用下的轨迹，记作Ek。即K在G的作用下所能变化成的所有元素的集合。.
这个时候有：|Ek|*|Zk|=|G|成立(k=1,2,…..n)。
C(π)：对于一个置换π∈G,及a∈X，若π(a)=a，则称a为π的不动点。π的不动点的全体记为C(π)。例如π=(123)(3)(45)(6)(7)，X={1,2,3,4,5,6,7};那么C(π)={3,6,7}共3个元素。
Burnside引理：L=1/|G|(Z1+Z2+Z3+Z4+……Zk)=1/|G|(C(π1)+C(π2)+C(π3)+…..+C(πn))(其中k∈X,π∈G)。
Polya定理：设G={π1，π2，π3……..πn}是X={a1，a2，a3…….an}上一个置换群，用m中颜色对X中的元素进行涂色，那么不同的涂色方案数为：1/|G|*(m^C(π1)+m^C(π2)+m^C(π3)+…+m^C(πk)). 其中C(πk)为置换πk的循环节的个数。

#define N 100000
int prime[N];
bool is_prime[N];

int sieve(int n)
{
    int p = 0;
    for (int i = 0; i <= n; ++i) is_prime[i] = true;
    is_prime[0] = is_prime[1] = false;
    for (int i = 2; i <= n; ++i) {
        if (is_prime[i]) {
            prime[p++] = i;
            for (int j = 2 * i; j <= n; j += i)
                is_prime[j] = false;
        }
    }
    return p;
}

int phi(int n)
{
    int rea = n;
    for(int i = 0; prime[i] * prime[i] <= n; i++)
    {
        if(n % prime[i] == 0)
        {
            rea = rea - rea / prime[i];
            while (n % prime[i] == 0)  n /= prime[i];
        }
    }
    if(n > 1)
        rea = rea - rea / n;
    return rea;
}

ll polya(int m, int n)
{
    ll sum = 0;
    ll i;
    for (i = 1; i * i < n; ++i) {
        if (n % i == 0) {
            sum += phi(i) * pow(m, n / i);
            sum += phi(n / i) * pow(m, i);
        }
    }
    if (i * i == n) sum += phi(i) * pow(m, i);
    if (n & 1) sum += n * pow(m, n / 2 + 1);
    else sum += (pow(m, n / 2) + pow(m, n / 2 + 1)) * n / 2;

    return sum / 2 / n;
}

快速傅里叶变换(FFT):

https://blog.csdn.net/ggn_2015/article/details/68922404
用于计算多项式乘法O(nlogn)

#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<complex>
#include <iostream>
using namespace std;
typedef complex<double> cd;//复数类的定义
const int maxl=2094153;//nlogn的最大长度(来自leo学长的博客)
const double PI=3.14159265358979;//圆周率,不解释
cd a[maxl],b[maxl];//用于储存变换的中间结果
int rev[maxl];//用于储存二进制反转的结果
void getrev(int bit){
    for(int i=0;i<(1<<bit);i++){//高位决定二进制数的大小
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
    }//能保证(x>>1)<x,满足递推性质
}
void fft(cd* a,int n,int dft){//变换主要过程
    for(int i=0;i<n;i++){//按照二进制反转
        if(i<rev[i])//保证只把前面的数和后面的数交换,(否则数组会被翻回来)
            swap(a[i],a[rev[i]]);
    }
    for(int step=1;step<n;step<<=1){//枚举步长的一半
        cd wn=exp(cd(0,dft*PI/step));//计算单位复根
        for(int j=0;j<n;j+=step<<1){//对于每一块
            cd wnk(1,0);//!!每一块都是一个独立序列,都是以零次方位为起始的
            for(int k=j;k<j+step;k++){//蝴蝶操作处理这一块
                cd x=a[k];
                cd y=wnk*a[k+step];
                a[k]=x+y;
                a[k+step]=x-y;
                wnk*=wn;//计算下一次的复根
            }
        }
    }
    if(dft==-1){//如果是反变换,则要将序列除以n
        for(int i=0;i<n;i++)
            a[i]/=n;
    }
}
int output[maxl];
char s1[maxl],s2[maxl];

void getmuti()    //计算高精度大数乘法，输入两个数a,b
{
    scanf("%s%s",s1,s2);//读入两个数
    int l1=strlen(s1),l2=strlen(s2);//就算"次数界"
    int bit=1,s=2;//s表示分割之前整块的长度
    for(bit=1;(1<<bit)<l1+l2-1;bit++){
        s<<=1;//找到第一个二的整数次幂使得其可以容纳这两个数的乘积
    }
    for(int i=0;i<l1;i++){//第一个数装入a
        a[i]=(double)(s1[l1-i-1]-'0');
    }
    for(int i=0;i<l2;i++){//第二个数装入b
        b[i]=(double)(s2[l2-i-1]-'0');
    }
    getrev(bit);fft(a,s,1);fft(b,s,1);//dft
    for(int i=0;i<s;i++)a[i]*=b[i];//对应相乘
    fft(a,s,-1);//idft
    for(int i=0;i<s;i++){//还原成十进制数
        output[i]+=(int)(a[i].real()+0.5);//注意精度误差
        output[i+1]+=output[i]/10;
        output[i]%=10;
    }
    int i;
    for(i=l1+l2;!output[i]&&i>=0;i--);//去掉前导零
    if(i==-1)printf("0");//特判长度为0的情况
    for(;i>=0;i--){//输出这个十进制数
        printf("%d",output[i]);
    }
    putchar('\n');
}

void getpoly()    //计算多项式乘法
{
    int n,m;
    scanf("%d%d",&n,&m);    //输入量多项式最高项次数
    for(int i=0;i<=n;i++) scanf("%lf",&a[i].real());    //读入第一个多项式的系数(a0+a1*x+a2*x^2+a3*x^3+.....+an*x^n)
    for(int i=0;i<=m;i++) scanf("%lf",&b[i].real());    //读入第二个多项式的系数(b0+b1*x+b2*x^2+b3*x^3+.....+bn*x^n)
    int bit=0,s=1;//s表示分割之前整块的长度
    for(s=1;s<=n+m;s<<=1)
        bit++;
    getrev(bit);fft(a,s,1);fft(b,s,1);//dft
    for(int i=0;i<s;i++)a[i]*=b[i];//对应相乘
    fft(a,s,-1);//idft
    for(int i=0;i<=n+m;i++)
        printf("%d ",(int)(a[i].real()+0.5));   //表示乘完多项式各项的系数，(a0+a1*x+a2*x^3...)
}

int main(){
    getmuti();     //10*10=100
    getpoly();    //(1+2x)*(1+2x+x2)=1+4x+5x2+2x3
    return 0;
}