参考博客:点击打开链接
- SVM的优缺点
优点:泛化错误率低,计算开销不大,结果容易解释
缺点:对参数的调节和核函数的选择敏感,原始分类器不佳修改仅适用于处理二分类问题
- SVM的目的:找到一个超平面,也就是分类的决策边界,使得离超平面最近的点尽可能的远,而那些最近的点就是支持向量
- 如何寻找最大间隔:
分隔超平面的形式: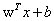
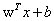
点到分隔超平面的距离: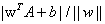
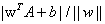
分类标签为:+1 和-1
间隔的计算方式可以表示为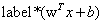
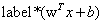
1>先找到最小间隔的数据点,然后将间隔最大化
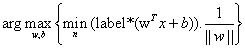
2>优化求解
由于对乘积进行优化是一件很讨厌的事情,因此我们要做的是固定其中一个因子而最大化其他因子。如果令所有支持向量的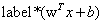
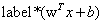
都为1那么就可以通过求1/ |w||的最大值来得到最终解
但是,并非所有数据点的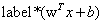 都等于1,只有那些离分隔超平面最近的点得到的
都等于1,只有那些离分隔超平面最近的点得到的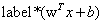 值才为1。而离超平面越远的数据点,其
值才为1。而离超平面越远的数据点,其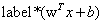 的值也就越大.
的值也就越大.
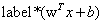 都等于1,只有那些离分隔超平面最近的点得到的
都等于1,只有那些离分隔超平面最近的点得到的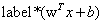 值才为1。而离超平面越远的数据点,其
值才为1。而离超平面越远的数据点,其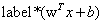 的值也就越大.
的值也就越大.3>转化为带约束条件的最优问题
约束条件为: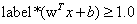
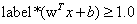
引入拉格朗日乘子:
- 将目标函数转化为基于超平面的数据点形式:
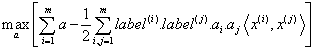
- 约束条件:
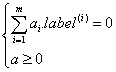
- 引入松弛变量C:用于控制最大化间隔,保证大部分的函数间隔小于1.0,引入松弛变量的意义在于允许一部分数据分到错误的一类中去
约束条件变为:
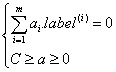
4>求解算法:SMO(SequentialMinimalOptimization) 序列最小优化
5>求解目标:alpha , b => 权重w
6>工作原理:

7>简化版SMO
算法思路:
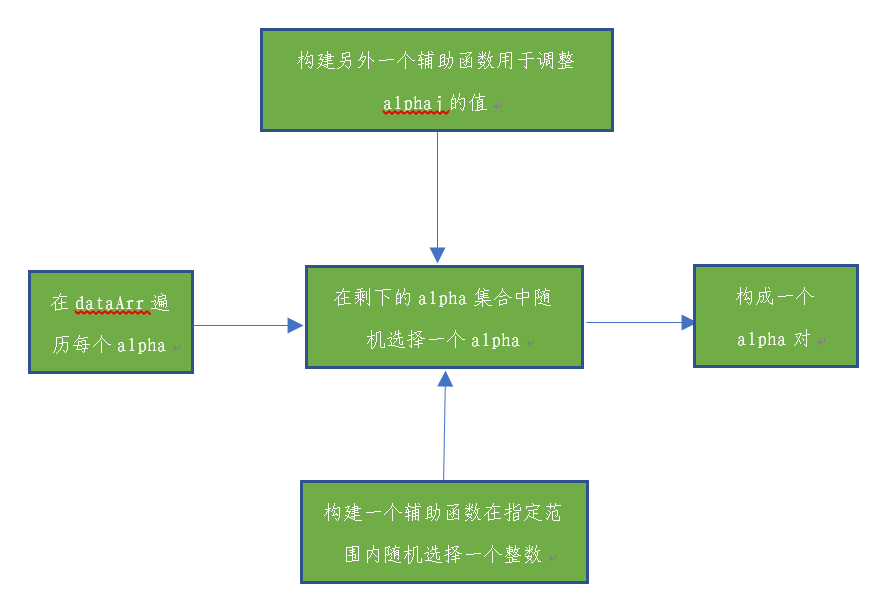
辅助函数:
#读取文本,分隔数据集和标签集
def loadDataSet(fileName):
dataMat = [];
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split(' ')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
#在一个范围内随机选择一个整数
#i为alpha的下标,m表示所有alpha的数目
def selectJrand(i,m):
j=i #we want to select any J not equal to i
while (j==i):
j = int(random.uniform(0,m))
return j
#用于调整大于alpha或者小于alpha的值
def clipAlpha(aj,H,L):
#如果alpha大于最大值,就将最大值赋值给alpha
if aj > H:
aj = H
#如果alpha小于最小值
if L > aj:
#就将最小值L赋值给alpha
aj = L
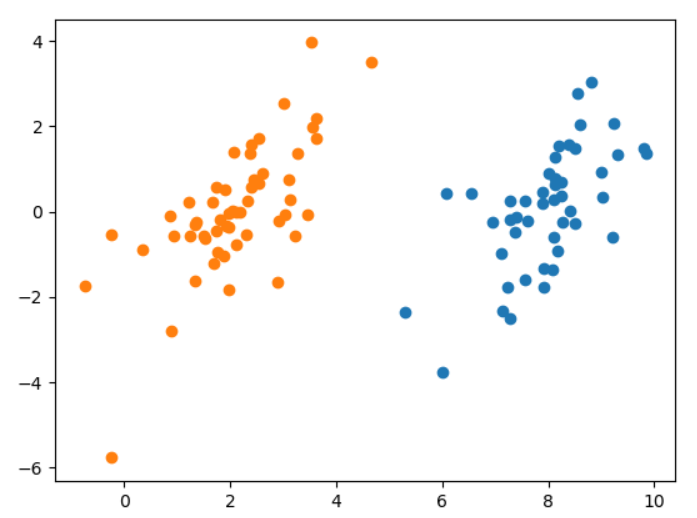
return aj首先画出原始数据集的散点图
#画出散点样本图
#画出散点样本图
def showDataSet(dataMat, labelMat):
data_plus = [] #正样本
data_minus = [] #负样本
#遍历所有的样本
for i in range(len(dataMat)):
#如果是正样本
if labelMat[i] > 0:
#将该样本数据添加到正样本的列表中
data_plus.append(dataMat[i])
else:
#如果是负样本,添加到负样本的列表中
data_minus.append(dataMat[i])
#分别将正负列表转为numpy矩阵
data_plus_np = np.array(data_plus) #转换为numpy矩阵
data_minus_np = np.array(data_minus) #转换为numpy矩阵
#np.transpose(data_plus_np)[0]取出第一列的值 作为x
# np.transpose(data_plus_np)[1]取出第二列的值 作为y
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1]) #正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) #负样本散点图
plt.show()
简化版SMO代码
#dataMatIn数据集 classLabels类别标签 常数C 容错率toler 取消前最大循环次数maxIter
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
#将数据集集合转为矩阵
dataMatrix = mat(dataMatIn);
#将标签集合转为矩阵之后转置
labelMat = mat(classLabels).transpose()
b = 0;
#取出数据集的行数和列数
m,n = shape(dataMatrix)
#构建一个alpha列矩阵,初始化为0
alphas = mat(zeros((m,1)))
#迭代次数iter
iter = 0
#当迭代次数小于最大迭代次数
while (iter < maxIter):
alphaPairsChanged = 0
#遍历所有的数据实例
for i in range(m):
#multiply函数是对应元素相乘和矩阵乘法*不同
#matrix:矩阵的转置
fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
#预测结果与实际的差值
Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions
#如果差值超过了容错率,对该数据实例对应的alpha值进行优化
#正间隔和负间隔都会被测试
#同时检测alpha的值不能等于0或者C,并且alpha的值也在区间(0,C)
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
#随机选择另外一个样本
j = selectJrand(i,m)
#重新预测该实例的所属类别
fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
#计算预测值和实际值的差值
Ej = fXj - float(labelMat[j])
#将两个样本的alpha值复制
#后面会对alpha[i]和alpha[j]的新旧值进行比较
#这里为新的alpha值重新分配内存空间,
alphaIold = alphas[i].copy();
alphaJold = alphas[j].copy();
#调整L,H,用于将alpha调整到0-C之间
#保证alpha在0-c之间
#确定alpha的最大最小值
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H:
print ("L==H");
#本次循环结束,进入下一循环
continue
#eta 是alpha[j]的最优修改量
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
#如果最优修改量>=0 跳出循环过程
if eta >= 0:
print ("eta>=0");
continue
#调整alpha
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
#调整大于或者小于H,L的alpha值
alphas[j] = clipAlpha(alphas[j],H,L)
#检查alpha[j]是否有轻微改变
if (abs(alphas[j] - alphaJold) < 0.00001):
print ("j not moving enough");
#如果是,则退出for循环
continue
#对i进行修改,修改量和j相同,但方向相反
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
#the update is in the oppostie direction
#在给alpha[i]和alpha[j]进行优化之后,设置一个常数项
#设置常数项
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
#如果程序一直不执行continue语句,一直执行for循环到这里
#那么表示现在就成功更改一对alpha
alphaPairsChanged += 1
#当循环到达maxiter的时候退出
print ("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
#iter:没有任何alpha改变的时候遍历数据集的次数
print ("iteration number: %d" % iter)
return b,alphas
运行svm.py文件
import svm
>>> dataArr,labelArr= svm.loadDataSet('E:\Python36\testSet.txt')b,alphas = svm.smoSimple(dataArr,labelArr,0.6,0.001,40)
>>> alphas[alphas>0]//数组过滤,只针对numpy数组有用
matrix([[ 2.23337801e-02, 1.28309399e-01, 1.83924318e-01,
1.33015764e-01, 2.01551733e-01, 8.67361738e-19]])>>> b
matrix([[-3.6218148]])
>>>
>>>
>>> from numpy import *
>>> shape(alphas[alphas>0])
(1, 6)
>>>>>> for i in range(100):
... if alphas[i]>0.0:
... print(dataArr[i],labelArr[i])
...
[4.658191, 3.507396] -1.0
[3.223038, -0.552392] -1.0
[3.457096, -0.082216] -1.0
[5.286862, -2.358286] 1.0
[6.080573, 0.418886] 1.0
[6.543888, 0.433164] 1.0
>>>#求解回归系数w
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr);
labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w>>> w=svm.calcWs(alphas,dataArr,labelArr)
>>> w
array([[ 0.82174458],
[-0.2691153 ]])
>>>def showDataSet(dataMat, labelMat,w,b,alphas):
data_plus = [] #正样本
data_minus = [] #负样本
#遍历所有的样本
for i in range(len(dataMat)):
#如果是正样本
if labelMat[i] > 0:
#将该样本数据添加到正样本的列表中
data_plus.append(dataMat[i])
else:
#如果是负样本,添加到负样本的列表中
data_minus.append(dataMat[i])
#分别将正负列表转为numpy矩阵
data_plus_np = np.array(data_plus) #转换为numpy矩阵
data_minus_np = np.array(data_minus) #转换为numpy矩阵
#np.transpose(data_plus_np)[0]取出第一列的值 作为x
# np.transpose(data_plus_np)[1]取出第二列的值 作为y
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1]) #正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) #负样本散点图
#=====绘制直线============#
#第一个特征值的的最大值
x1 = max(dataMat)[0]
#第一个特征值的最小值
x2 = min(dataMat)[0]
#将权重赋值给a1,a2
a1,a2 = w
b = float(b)
#取出第一个权重系数
a1 = float(a1[0])
a2 = float(a2[0])
#根据第一个特征值的最大最小值x1,x2求出第二个特征值的最大最小值y1,y2
#y1*a2+x1*a1+b=0
#y2*a2+x2*a1+b=0
y1,y2 = (-b - a1 * x1)/a2,(-b - a1*x2)/a2
plt.plot([x1,x2],[y1,y2])
#========找出支持向量点==========#
for i, alpha in enumerate(alphas):
if abs(alpha) > 0:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.show()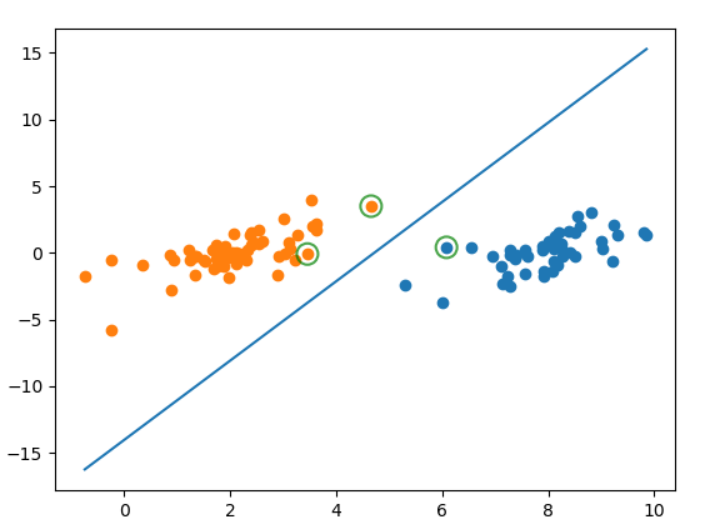
8>完整版的SMO
优化点 =》 alpha的选择
算法思路:
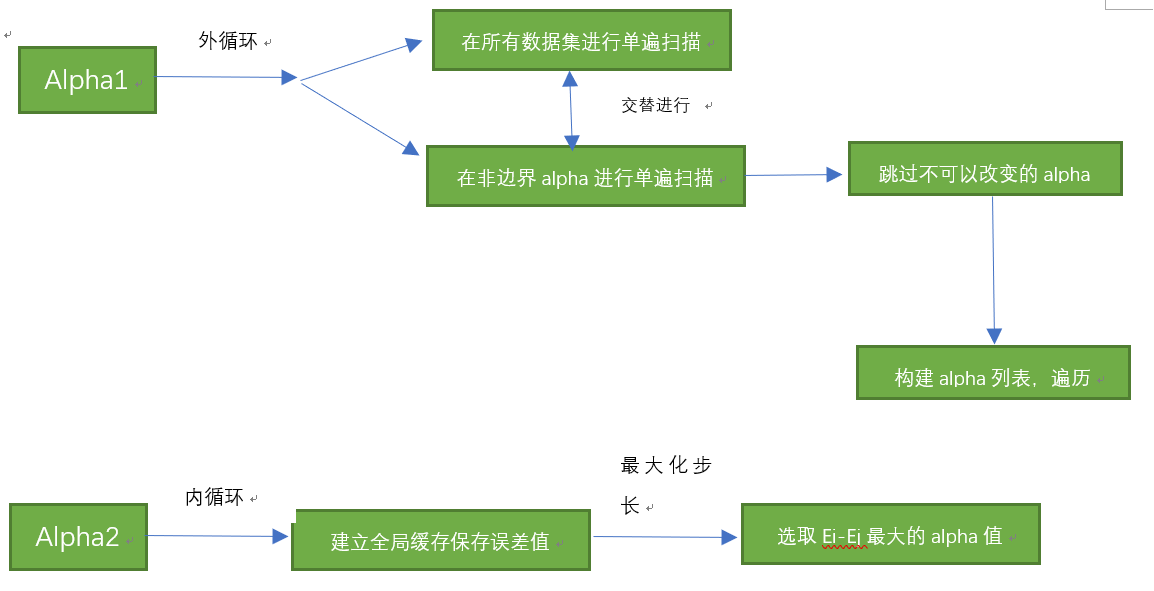
构建辅助函数:
#构建一个结构体,用来存储后面需要的所有的数据变量
class optStruct:
#dataMatIn数据集 classLabels类别标签 常数松弛变量C 容错率toler
def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
#取出数据集的行
self.m = shape(dataMatIn)[0]
#初始化alphas的值为0
#(self.m,1)创建一个m行1列的零矩阵
self.alphas = mat(zeros((self.m,1)))
self.b = 0
#初始化误差缓存为(self.m,2)m行2列的零矩阵
#第一列是有效标志位,第二列是实际的误差值
self.eCache = mat(zeros((self.m,2))) #first column is valid flag
#创建一个(self.m,self.m)m行m列的零矩阵
self.K = mat(zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
#返回计算的误差
#oS为结构体
def calcEk(oS, k):
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
#计算误差
Ek = fXk - float(oS.labelMat[k])
return Ek
#通过最大步长得到第二个alpha的值--->内循环中的启发式方法
"""
参考博客:http://colabug.com/1640061.html
"""
#i为第一个alpha的下标
#os为结构体
#Ei为第i个元素的误差
def selectJ(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej
maxK = -1;
maxDeltaE = 0;
Ej = 0
#将误差值Ei在缓存中设置为有效的
#这里的有效意味着它已经计算好了
oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E
#nonzero返回不为零的元素的下标 元组存储每列的下标
#取出eCache误差缓存中的第一列元素的非零值的行维度的索引值
validEcacheList = nonzero(oS.eCache[:,0].A)[0]
'''
a = [[1,2,4],[2,3,4],[3,4,5]]
a = mat(a)
b = a.flatten()
print(b)
c = a.flatten().A
print(c)
d = a.flatten().A[0]
print(d)
[[1 2 4 2 3 4 3 4 5]]
[[1 2 4 2 3 4 3 4 5]]
[1 2 4 2 3 4 3 4 5]
# from numpy import *
# a = [[0,0,4],
# [2,0,4],
# [0,4,5]]
# a = mat(a)
# c = nonzero(a.A)
# print(c[0])#[0 1 1 2 2]
返回两个元组的数组,一个是所有非零元素行维度的索引值,,另外一个是非零元素列维度的索引值
(array([0, 1, 1, 2, 2], dtype=int64), array([2, 0, 2, 1, 2], dtype=int64))
'''
#如果存在不为零的误差
if (len(validEcacheList)) > 1:
#遍历所有误差
for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E
#如果等于i,不再往下计算i的误差,浪费时间
#继续进行for循环
if k == i:
continue #don't calc for i, waste of time
#计算误差
Ek = calcEk(oS, k)
#得到误差的差值
deltaE = abs(Ei - Ek)
#选择具有最大步长的j
#如果差值大于maxDeltaE
if (deltaE > maxDeltaE):
maxK = k;
maxDeltaE = deltaE;
Ej = Ek
return maxK, Ej
#如果不存在不为0的误差,随机选择一个整数作为j
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
#得到误差Ej
Ej = calcEk(oS, j)
return j, Ej
#计算Ek,更新误差缓存
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]alpha2选择,内循环(最大步长):
#优化的SMO算法,返回0 没有alpha对的值发生改变,返回1 有alpha对的值发生改变
def innerL(i, oS):
#索引值为i的误差
Ei = calcEk(oS, i)
#如果差值超过了容错率,对该数据实例对应的alpha值进行优化
#正间隔和负间隔都会被测试
#同时检测alpha的值不能等于0或者C,并且alpha的值也在区间(0,C)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
#通过内循环启发式学习找到第二个alpha的值,并计算误差Ej
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
#将两个样本的alpha值复制
#后面会对alpha[i]和alpha[j]的新旧值进行比较
#这里为新的alpha值重新分配内存空间,
alphaIold = oS.alphas[i].copy();
alphaJold = oS.alphas[j].copy();
#调整L,H,用于将alpha调整到0-C之间
#保证alpha在0-c之间
#确定alpha的最大最小值
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H:
print ("L==H");
return 0
#eta 是alpha[j]的最优修改量
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
if eta >= 0:
print ("eta>=0");
return 0
#如果最优修改量小于0,则对alpha[j]进行修改调整
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
# 调整大于或者小于H,L的alpha值
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
#更新误差值Ej
updateEk(oS, j) #added this for the Ecache
#检查alpha[j]是否有轻微改变
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print ("j not moving enough");
return 0
#对i进行修改,修改量和j相同,但方向相反
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
#更新Ei,这次修改和Ej是相反的方向
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
#设置常数项
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
#如果alpha[i]在区间[0,C]中
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1
#否则如果alpha[j]在区间[0,C]中
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2)/2.0
#返回1,有任意一对alpha值发生变化
return 1
else:
#返回0,没有alpha值发生变化
return 0外循环
#完整的SMO算法外循环代码
#dataMatIn:数据集 classLabels标签集, C松弛变量 , toler容错率, maxIter最大迭代次数,kTup=('lin', 0)线性核函数 初始值为0
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #full Platt SMO
#利用输入参数构建一个结构体
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
#初始化迭代次数为0
iter = 0
entireSet = True;
#初始化改变的alpha值对数为0
alphaPairsChanged = 0
#当迭代次数小于最大迭代次数 并且有alpha对的值改变 或者entireset等于true
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
#初始化改变的alpha值对数为0
alphaPairsChanged = 0
if entireSet: #go over all
#遍历所有值
for i in range(oS.m):
#innerL(i,oS)优化的SMO算法,返回0 没有alpha对的值发生改变,返回1 有alpha对的值发生改变
#alphaPairsChanged统计改变的alpha对值的数量
alphaPairsChanged += innerL(i,oS)
#打印迭代次数itera,样本i,多少对alpha值改变
print ("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
else:#遍历非边界值
#go over non-bound (railed) alphas
#否则entireset等于false遍历非边界的alphas值
#统计alpha值不等于0,并且在[0,C]范围内的值的行维度列表
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
#统计非边界的alpha值对改变的对数
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print ("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
#遍历一次后改为非边界遍历
if entireSet:
entireSet = False #toggle entire set loop
#如果alpha对值改变数量为0
#这里无论alpha值对是否改变,将会对整个集合的一次遍历计成一次迭代
#如果本来就是非边界遍历,并且alpha对改变数为0,则切换到完整遍历
elif (alphaPairsChanged == 0):
entireSet = True
#打印出迭代次数
print ("iteration number: %d" % iter)
return oS.b,oS.alphas运行svmCOM.py
>>> reload(svmCOM)
<module 'svmCOM' from 'E:\Python36\svmCOM.py'>
>>> dataArr,labelArr= svmCOM.loadDataSet('E:\Python36\testSet.txt')
>>> svmCOM.smoP1(dataArr,labelArr,0.6,0.001,40)
L==H
fullSet, iter: 0 i:0, pairs changed 0
L==H
fullSet, iter: 0 i:1, pairs changed 0
fullSet, iter: 0 i:2, pairs changed 0
fullSet, iter: 0 i:3, pairs changed 0
fullSet, iter: 0 i:4, pairs changed 0