约瑟夫问题求解
来源:http://dsalgo.openjudge.cn/
总时间限制:1000ms 内存限制:65536KB
描述
有n只猴子,按顺时针方向围成一圈选大王(编号从1到n),从第1号开始报数,一直数到m,数到m的猴子退出圈外,剩下的猴子再接着从1开始报数。就这样,直到圈内只剩下一只猴子时,这个猴子就是猴王,编程求输入n,m后,输出最后猴王的编号。
输入
输入包含两个整数,第一个是n,第二个是m(0<m,n<=300)。
输出
输出包含一行,即最后猴王的编号。
样例输入
12 4
样例输出
1
解法一:
常规解法,用循环单向链表存储并模拟选猴王的过程。问题可以抽象为,
有编号为1~n的n个元素,按顺序分别存储在循环单向链表list的结点的数据中。从list的位序为0的结点开始计数0,删除计数到m-1的结点,并以后继作为新的计数起点,然后重复,直至最后只剩一个节点。
注意:
1) 如果m>=list.length,则循环到表头部分,不妨令m’=m%list.length,即为新计数起点对应结点的位序;
2) 考虑到每次都是删除的(m-1)%list.length节点,不妨将其后继节点设置为链表的第0号结点;
步骤:
1) 输入n, m,构造L;
2) 判断链表长度list.length是否==1,如果是,则返回L[0].data值,即为求解编号;如果不是,则删除m’(m’=m%length)的前驱L[(m-1)%length],list.length—
3) 以m’为新链表的第0号结点,跳转至2),直到list.length==1;
伪码(循环实现)
// Java代码
/**
* 约瑟夫问题通过模拟计数进行求解
* @param n 参与人数
* @param m 每次报的最大号, 也是要删除的号
* @return 最后胜出者编号
*/
static int JosephCount(int n, int m){
CLinkedList list = new CLinkedList();
// 构造n个数据结点组成的带头节点的链表, 数据域分别为1, 2, 3... n
for(int i = n; i > 0; i --){
list.add(0, i); // 在第0号位置插入新节点
}
int removeIndex = 0; // 要删除的结点位序
int newFirsdNodeIndex = 0; // 新链表0号位置结点在设置新0号结点前的链表中的位置
// 循环报号过程: 删除m-1位置结点, 设置链表0号结点, 直到只剩1个结点
while(list.getLength() > 1){
removeIndex = (m-1) % list.getLength();
list.remove(removeIndex);
// 删除之后, length--, 原removeIndex可能等于length
if(removeIndex == list.getLength()){
// 如果删除结点是尾节点, 新链表0号结点也是删除结点后的链表0号结点
newFirsdNodeIndex = 0;
}
else{
// 删除节点不是尾节点, 新链表0号结点位序是删除结点位序
newFirsdNodeIndex = removeIndex;
}
list.setFirstNode(newFirsdNodeIndex);
}
int winId = list.getNode(0).getData(); // 最后只剩1个数据结点的data域即为胜出者编号
return winId;
}
解法二:
递推公式,这里用递归实现
分析
解法一过程中,发现每次删除的都是第m-1结点,m结点成为新表0号结点,左半部分右移,右半部分左移。能不能找到第k次和k-1次之间的关系?或者长度len和len-1之间的关系?
以n=12, m=4为例,
|
操作状态 |
剩余编号序列 |
长度len |
|
原始编号 |
1 2 3 4 5 6 7 8 9 10 11 12 |
12 |
|
第一次 删除 设置0结点 |
1 2 3 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 1 2 3 |
11 |
|
第二次 删除 设置0结点 |
5 6 7 9 10 11 12 1 2 3 9 10 11 12 1 2 3 5 6 7 |
10 |
|
第三次 删除 设置0结点 |
9 10 11 1 2 3 5 6 7 1 2 3 5 6 7 9 10 11 |
9 |
|
… |
|
|
|
第k-1次 删除 设置0结点 |
k0 k1 k2 … k(m-2) k(m-1) km k(m+1)… k(len-2) k(len-1) |
n-(k-1) |
|
第k次 删除 设置0结点 |
k0 k1 k2 … k(m-2) km k(m+1)… k(len-2) k(len-1) km k(m+1)… k(len-2) k(len-1) k0 k1 k2 … k(m-2) |
n-k |
|
… |
|
|
具体地,
从初始状态到第一次设置0结点,位置为4~11的元素(编号5~12)变成了0~7,也就是左移m (m=4);位置为0~2的元素(编号1~3)变成了8~10,也就是右移n-m (n-m=8);
第一次设置0结点到第二次设置时,位置4~10的元素位置变成0~6,即左移m (m=4);位置0~2的元素位置变成7~9,即右移n-1-m (n-1-m=7);
从第k-1次设置0结点,到第k次设置0结点时,
当k次操作前的位置i<m-1时,表长=n-(k-1),操作后的位置相当于向右移动n-k-m,表长度=n-k;
当k次操作前的位置i>m-1时,表长=n-(k-1),操作后的位置相当于向左移动m,表长度=n-k;
如果记元素在第k次的位置为f(k)(k>=1),那么有,
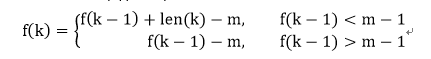
表长,

f(k)是元素在表中位置,可知0<=f(k)<len(k),那么
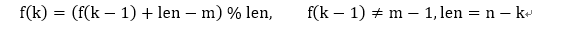
要求解的是什么?
要求的是胜出者编号,知道k=0时,元素编号=位置f(k=0)+1,而不知胜出者位置。不妨记胜出者元素编号为X(X保持不变),问题转化为求f(k=0)。
还有个隐含情况,k=n-1时(长度=1),胜出者位置即为唯一元素位置f(k=n-1, X)=0。
这刚好可以利用递推关系求解,
问题转化为
条件:
1) 已知f(n-1) = 0;
2) f(k)和f(k-1)关系,

求解:f(0)
求解过程
由2)可得,
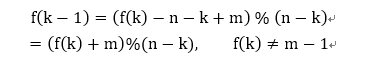
可以用递归来实现,伪码(JAVA)
/**
* 调用递推公式函数, 求解胜利者初始位置, 转换为编号并返回
*/
static int JosephCount_Recursion(int n, int m){
return JosephCount_f(0, n, m) + 1;
}
/**
* 利用递归实现递推公式求解f(0)
*/
static int JosephCount_f(int k, int n, int m){
if(k == n-1) return 0;
else{
return (JosephCount_f(k+1, n, m) + m) % (n-k);
}
}
当然,可以将关于操作次数k的位置函数f(k),转化为关于长度的位置函数f(t)。
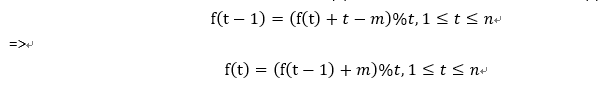
问题也就转化为已知f(1)=0,求解f(n)了。具体过程不再给出,下面给出伪码(JAVA)。
/**
* 调用递推公式函数, 求解胜利者初始位置, 转换为编号并返回
*/
static int JosephCount_Recursion2(int n, int m){
int winId = JosephCount_f2(n, m) + 1;
return winId;
}
/**
* 利用递归实现递推公式求解f(1)
*/
static int JosephCount_f2(int n, int m){
if(n == 1){
return 0;
}
else{
return (JosephCount_f2(n-1, m) + m) % n;
}
}
demo源码下载地址:Github代码