只看题目描述 你会发现这是一道非常简单的 dp 题
但是 数据范围是 L≤109 啊
30分解:
就是很简单的啊
30分 View Code1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define go(i,a,b) for(register int i=a;i<=b;i++) 5 #define yes(i,a,b) for(register int i=a;i>=b;i--) 6 #define mem(a,b) memset(a,b,sizeof(a)); 7 #define ll long long 8 #define db double 9 using namespace std; 10 int read() 11 { 12 int x=0,y=1;char c=getchar(); 13 while(c<'0'||c>'9') {if(c=='-') y=-1;c=getchar();} 14 while(c>='0'&&c<='9') {x=(x<<1)+(x<<3)+c-'0';c=getchar();} 15 return x*y; 16 } 17 int l,s,m,t; 18 ll ans,dp[300000]; 19 bool f[300000]; 20 int main() 21 { 22 l=read();s=read();t=read();m=read();mem(dp,77);ans=2100000000; 23 go(i,1,m) f[read()]=1; 24 if(!f[0]) dp[0]=0;else dp[0]=1; 25 go(i,1,l+t) 26 { 27 go(j,s,t) 28 { 29 if(i-j<0) continue ; 30 dp[i]=min(dp[i],dp[i-j]+(f[i]==1)); 31 } 32 if(i>=l) ans=min(ans,dp[i]); 33 } 34 printf("%lld",ans); 35 return 0; 36 }
再讲一下我自己想的方法（但是写了好久代码也写不对qwq）：
前面的方法中 for(j,s,t) dp[i]=min(dp[i],dp[i-j]) (如果i处有石头就再+1)
发现要求dp[i] 只要知道dp[i-t]~dp[i-s] 即可 前面的都对现在没有影响
s,t<=10 范围非常小就可以不要开之前的dp[]数组了
又发现只要求 min(dp[i-t]~dp[i-s])
好像滑动窗口啊！！！
为了方便还可以用deque和queue
我觉得我说的好有道理啊 但是我写不对qwq
$upd on 11.2:$我以前在想啥?这样显然过不了吖$QwQ$
我看懂的题解：
我们发现不能直接像之前30分的做法那样DP
是因为L实在是太大了 开不了那么大的数组
所以我们就想能不能把L变得小一点
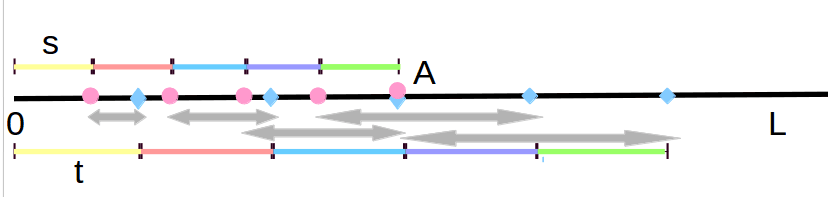
如图 显然灰色箭头是可以走得到的地方（第i步走的最近和走的最远之间的）
起初还有灰色箭头覆盖不到的地方
但是我们可以发现当红色点和蓝色点重合之后 灰色箭头一定可以覆盖到后面的每一个点
而重合点即为s和t的最小公倍数lcm
当两块石头之间的间隔大于lcm时 直接把它压缩成lcm
但是要注意一种特殊的情况 就是当s==t时 特判即可
CODE
View Code1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define go(i,a,b) for(register int i=a;i<=b;i++) 6 #define mem(a,b) memset(a,b,sizeof(a)); 7 #define M 90*100+10 8 #define N 100+10 9 using namespace std; 10 int read() 11 { 12 int x=0,y=1;char c=getchar(); 13 while(c<'0'||c>'9') {if(c=='-') y=-1;c=getchar();} 14 while(c>='0'&&c<='9') {x=(x<<1)+(x<<3)+c-'0';c=getchar();} 15 return x*y; 16 } 17 int l,s,m,t,ans,a[N],b[N],dp[M]; 18 bool f[M]; 19 int main() 20 { 21 l=read();s=read();t=read();m=read();mem(dp,77);dp[0]=0;ans=210; 22 go(i,1,m) a[i]=read(); 23 sort(a+1,a+m+1); 24 if(s==t) 25 { 26 ans=0; 27 go(i,1,m) if(!(a[i]%s)) ans++; 28 printf("%d",ans); 29 return 0; 30 } 31 go(i,1,m) 32 { 33 if(a[i]-a[i-1]>s*t) b[i]=b[i-1]+s*t; 34 else b[i]=b[i-1]+a[i]-a[i-1]; 35 f[b[i]]=1; 36 } 37 l=b[m]+t*s; 38 go(i,1,l) 39 { 40 go(j,s,t) 41 { 42 if(i-j<0) continue ; 43 dp[i]=min(dp[i],dp[i-j]+(f[i]==1)); 44 } 45 if(i>=b[m]) ans=min(ans,dp[i]); 46 } 47 printf("%d",ans); 48 return 0; 49 }
至此 洛谷普及训练场所有DP专题都通关啦(当然不是都完成了qwq)
^o^ 然后现在要去回顾一下原来写过的DP题