最近看到了Brett Beauregard发表的有关PID的系列文章,感觉对于理解PID算法很有帮助,于是将系列文章翻译过来!在自我提高的过程中,也希望对同道中人有所帮助。作者Brett Beauregard的原文网址:http://brettbeauregard.com/blog/2012/01/arduino-pid-autotune-library/
最后,我发布了一个Autotune库来补充Arduino PID库。当我发布当前版本的PID库时,我发布了一系列异常广泛的帖子,让人们对里面发生的事情更易理解。
虽然没有那么深入,但这是这个帖子的目标。我将解释 Autotune 库想要完成的任务,以及它是如何处理其业务的。
1、原由
几年来,我一直想拥有一个自动整定库,但由于我与雇主的协议,我无法写一个。但是!当我找到由William Spinelli编写的AutotunerPID工具箱时,我已经准备好了;我的公司对我移植和扩展现有的开源项目没有任何问题。
我将代码从 matlab 转换过来,对峰值识别代码进行了一些调整,并将其从标准形式 (Kc、Ti、Td) 切换到理想形式 (Kp、Ki、Kd)。除此之外,所有的功劳都归斯皮内利先生所有。
2、理论
PID 控制器的最佳整定参数 (Kp、Ki、Kd) 将取决于该控制器的驱动的是什么。烤箱最好的整定参数与低温烹饪器具最好的整定参数是不同的。
自整定器试图找出控制器驱动的内容的性质,然后从中进行调整参数。有多种方法可以做到这一点,但大多数方法都涉及到以某种方式更改 PID 输出,然后观察输入的响应方式。
库中使用的方法称为中继方法。下面是它的工作原理:
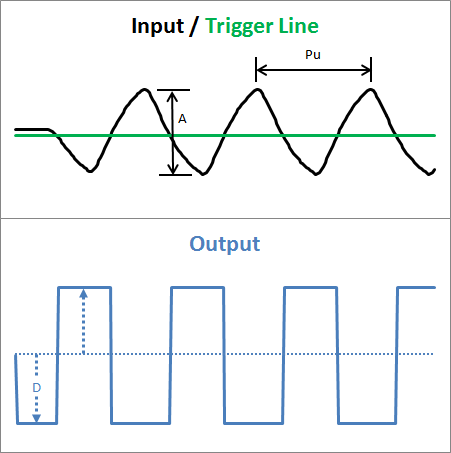
从稳态开始(输入和输出都是稳态),输出沿一个方向跨一定距离D阶跃,当输入越过触发线时,输出沿另一个方向跨距离D阶跃。
通过分析峰值的距离以及峰值相对于输出变化的大小,Autotuner 可以分辨出一种类型的过程和另一种类型的过程之间的区别。因此,不同的系统将获得自定义调优参数:
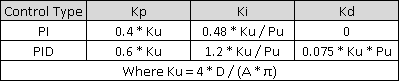
3、实施情况
这在理论上效果很好,但现实世界的数据并不是很合作。输入信号通常是嘈杂的,这会导致两个主要问题。
3.1、问题 #1:何时步进?
由于噪声信号是起伏的,当输入信号经过触发线时,触发线很可能会被交叉几次。这可能会导致输出中轻微的颤振,如果严重的话,可能会完全破坏:
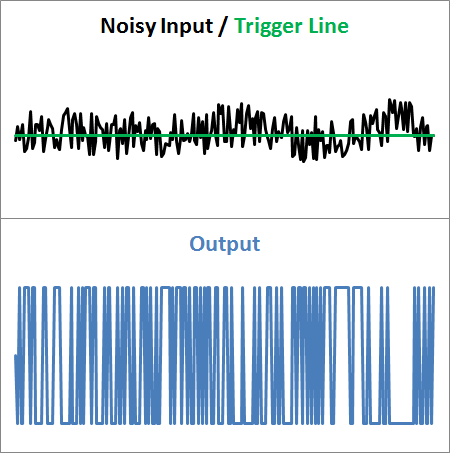
我选择回避此问题的方式是让用户指定噪声带。实际上,这将创建两条触发线。由于它们之间的距离等于噪音 (如果设置得当),由于信号抖动而发生多次交叉的可能性较小。
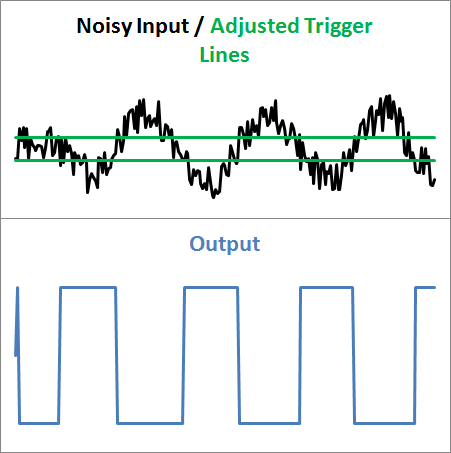
3.2、问题 #2:峰值识别
在模拟世界中,识别峰值很容易: 当输入信号改变方向时,这是最小值或最大值 (取决于发生的更改)。但是,在嘈杂的世界中,此方法失败:
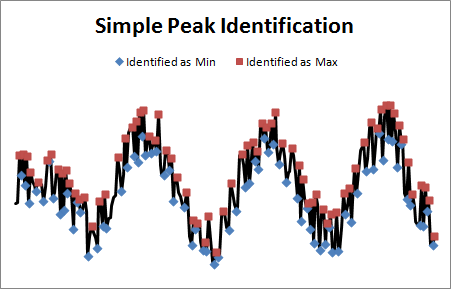
每一个噪声信号都是一个方向的改变。为了处理这个问题,我添加了一个“回溯时间”参数。这是一个糟糕的名字。如果你能想出更好的办法,请告诉我。
无论如何,用户定义了某个窗口,比如10秒。然后,库将当前点与最后十秒的数据进行比较。如果它是最小值或最大值,则会将其标记为可能的峰值。
当标记的点从最大值切换到最小值时,反之亦然,以前标记的点被确认为峰值。
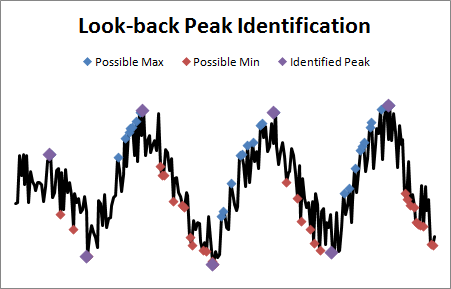
另一种解释回溯时间的方法是,如果一个点是一个回溯未来或过去中最大 (或最小) 的值,则该点将被标识为峰值。就像我说的:可怕的名字。
4、你也应该知道..。
执行的循环数将在3到10之间变化。该算法一直等到最后3个最大值彼此都在5%以内。这是为了确保我们已经达到了稳定的振荡并且没有外部奇异现象发生。这让我想到……
我不是Autotune的超级粉丝。我经常说,而且仍然相信,一个受过中等训练的人会很容易战胜自动整定器。如果不清楚算法的话,很多地方会很容易出错。话虽如此,但 Autotune 是帮助新手进入竞技场的宝贵工具。
欢迎关注:
