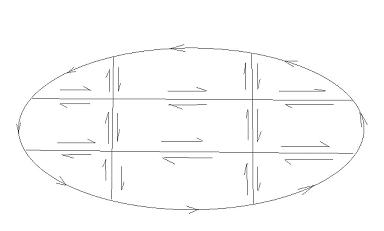
格林公式在物理上的意义就是闭合曲线Γ内所有微环流量(Microscopic circulation)的总和等于沿曲线Γ方向的线积分(Macroscopic circulation)。
假设平面上的闭合曲面S是连续平滑的,我们把S分割成无穷多个很小的微平面,每个微平面 xi都是被闭合的曲线包围的,假设包围S的曲线方向为逆时针的,那么我们假设每个微平面也是逆时针的,这样便有下面图:
假设每个微平面足够的小,我们可以发现内部的部分环流在作用场的作用下相互抵消了,所以所有的微环流量的总和等于沿曲线Γ方向的线积分。
接着带来了一个问题,怎么获得所有的微环流量呢?
不要急,我马上就解释:

上图是一个微环量的图,事实上它是一种模型的假设,肉眼是看不见的,它是非常非常小的,我们假设它接近于四边形,且平行于x,y轴。
速度场为F(x,y) = M(x,y) * i + N(x,y) * j;
F(x, y) * Δx * i = M(x,y) * Δx (1)
F(x + Δx, y) * Δy * j = N(x+Δx, y) * Δy (2)
F(x , y +Δy) * Δx * (-i) = -M(x, y+ Δy) * Δx (3)
F(x , y) * Δy * (-j) = - N(x,y)*Δy (4)
(2) - (4) 得到 (N(x + Δx, y) + N(x,y) )* Δy = ∂N/∂x*Δx * Δy (5)
(3) -(1)得到 -(M(x, y+ Δy) - M(x,y) )* Δx = -∂M/∂y * Δy * Δx (6)
5,6式同时除以面积Δx * Δy得到环流密度∂N/∂x - ∂M/∂y,看到这里大家大概应该明白格林公式是怎么一回事了。
Curl F * k = ∂N/∂x - ∂M/∂y (这里是点乘)
然后根据S面上的密度对S面进行积分,那么便有∫∫(∂N/∂x - ∂M/∂y)dS,
所以 ∫∫(∂N/∂x - ∂M/∂y)dS = ∮Mdx + Ndy;
stokes therom是格林公式的扩展形式,我们可以类似的进行论证。