假设我们把两个高斯函数相乘就像贝叶斯定理那样,一个先验概率,一个测量值的概率。
先验概率的平均值是mu,方差是omiga的平方,测量值的平均值是nu,方差是r的平方。
新的平均值和旧的平均值加权平均,mu给予权重r^2, nu给予权重omiga^2 。然后用权重因子归一化。
新的方差项omiga^2 是更新之后新的方差,由下面的方程给出。
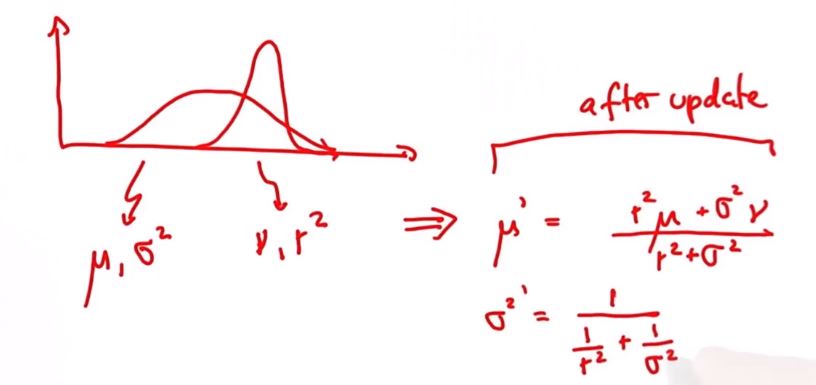
mu^2是之前均值的加权平均,很显然之前的高斯函数有更高的不确定性,所以omiga^2更大,
这就是说nu的权重比mu的权重大的多,所以这个平均值相对mu来说会更靠近nu.
有趣的是方差项不受实际的平均值影响,它只使用了之前的方差然后构建了一个更陡峭的新方差。
蓝色线表示的那样。
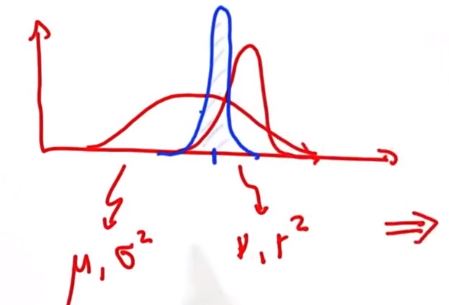
上面的两个公式就是卡尔曼滤波里对测量值的更新。
这是先验概率p(x),这是测量值的概率p(z/x),这里是后验概率p(x/z)。
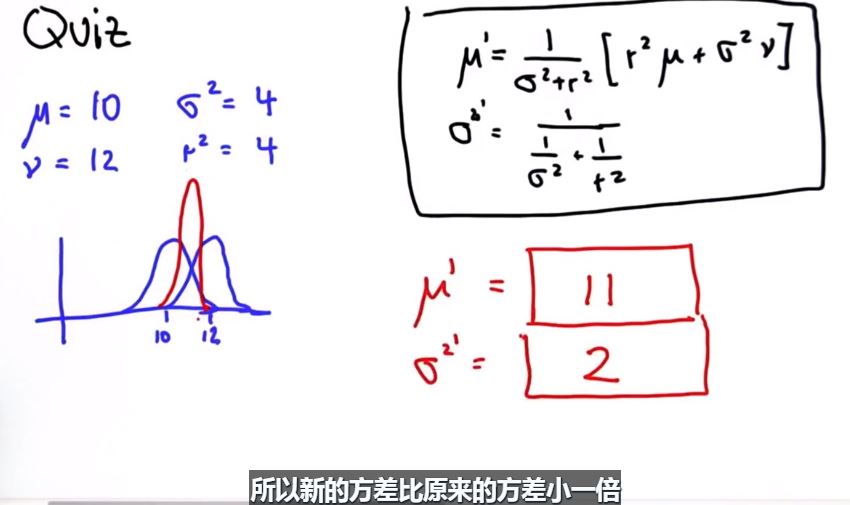
测试:用上面的两个公式更新均值和方差
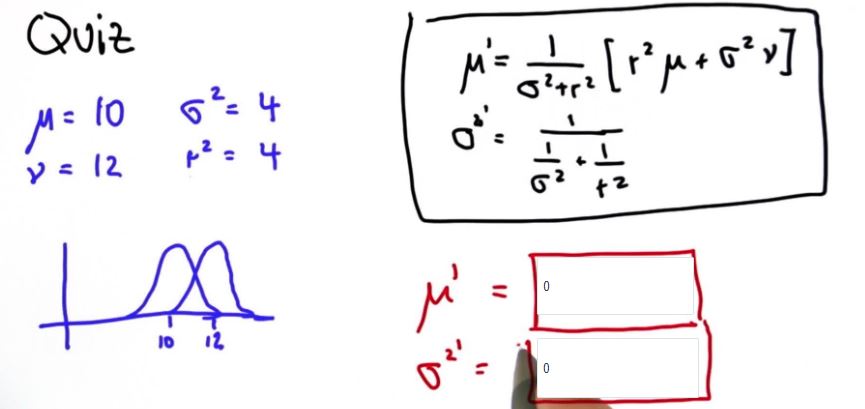
答案