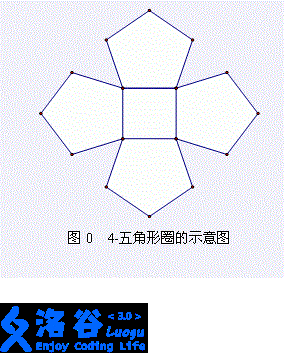
我们可以看一下题目中给的这张图。
首先,树是没有环的,所以我们要把所有的环上的边都删去一条。
我们可以现在每个五边形上删去一条边。
但删完之后我们会发现,里面还有一圈。
这时候,我们就要在这里面随便选一条边删去。
也就是,我们需要把n-1个五边形删去一条边,再把剩下的一个删掉两条边
那么方案数就是\(4 \times n \times 5 ^ {n-1}\)
补充:
可能有人会问,这难道不会多算吗?
我们再仔细分析一下。
为什么是\(4 \times n\) 而不是\(5 \times n\)
这个可以这么理解,删两条边的时候,我们强制删去里面的环的一条边,在删去一个五边形上的边就不会重了。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define LL long long
int n,t;
const int p = 2007;
LL ksm(LL a,LL b)
{
LL res = 1;
for(; b; b >>= 1)
{
if(b & 1) res = res * a % p;
a = a * a % p;
}
return res;
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
printf("%lld\n",n* 4 *ksm(5,n-1) % p);
}
return 0;
}
听说,这题还可以用矩阵树过去,但蒟蒻我不会QAQ。
不知不觉又水了一道题。