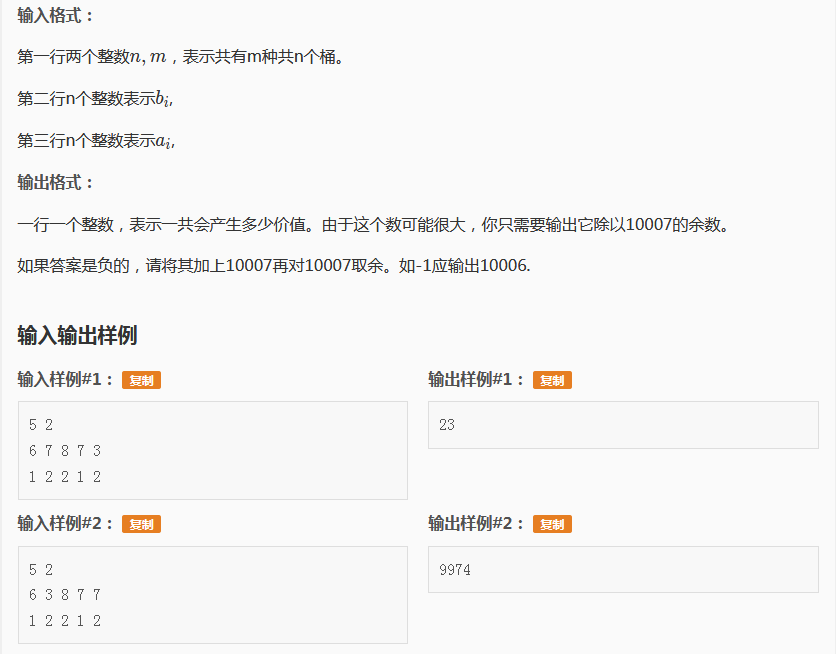
这是我们团队的一个题目(就是一个_rqy说很好写的题QwQ)
题目背景


这个题目的思路很玄学(性感_rqy在线讲解)
60 Pts
对于前面的六十分,好像很好拿,单纯的打一个模拟
唯一需要注意的地方就是要是想拿全60分,不能是简简单单的n3的枚举,这显然会T
那么问题就来了:
如何才能不T的夺得这三十呢???
我们发现,
其实y它并无卵用
所以只用枚举x和z就行了(当然需要满足3|x-z)
没错就是这样qwq
100 Pts
这个方法就是用一些操作来维护几个数组
我们发现,y对于价值的贡献为零,也就是说
我们可以将价值的公式展开进行进一步的操作
Σ(x+z)*(bx-bz)=∑x*bx+z*∑bx-bz*∑x-z*bz*∑1
这样我们就只需要维护这四个数组就可以了
对于这四个数组的维护
我们需要进行三次的循环(把x和z除以三同余的放在一组,这样的三组,一定满足x+y=z−2y)
分别对其进行维护
最终得到了答案
#include<bits/stdc++.h> using namespace std; inline int read() { int X=0,w=1; char c=getchar(); while(c<'0'||c>'9') { if(c=='-') { w=-1; } c=getchar(); } while(c>='0'&&c<='9') { X=(X<<3)+(X<<1)+c-'0'; c=getchar(); } return X*w; } const int mod=10007; const int maxn=100001; int a[maxn],b[maxn],c[maxn],d[maxn]; int m[maxn],n[maxn]; int x,y,ans; int main() { x=read(); y=read(); for(int i=1;i<=x;i++) { n[i]=read()%mod; } for(int i=1;i<=x;i++) { m[i]=read(); } for(int i=1;i<=3;i++) { memset(a,0,sizeof(a)); memset(b,0,sizeof(b)); memset(c,0,sizeof(c)); memset(d,0,sizeof(d)); for(int j=i;j<=x;j+=3) { ans=(ans+j%mod*c[m[j]]%mod)%mod; ans=(ans-n[j]*b[m[j]]%mod)%mod; ans=(ans+d[m[j]])%mod; ans=(ans-a[m[j]]*n[j]%mod*(j%mod)%mod)%mod; a[m[j]]=(a[m[j]]+1)%mod; b[m[j]]=(b[m[j]]+j)%mod; c[m[j]]=(c[m[j]]+n[j])%mod; d[m[j]]=(d[m[j]]+j%mod*n[j]%mod)%mod; } } printf("%d",(ans+mod)%mod); return 0; }