题目描述
对于1 位二进制变量定义两种运算:
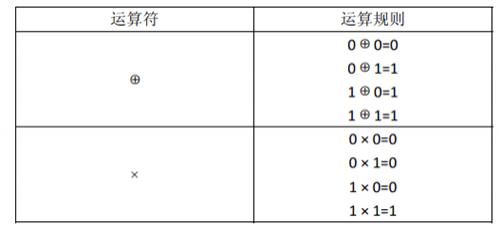
运算的优先级是:
-
先计算括号内的,再计算括号外的。
-
“× ”运算优先于“⊕”运算,即计算表达式时,先计算× 运算,再计算⊕运算。例如:计算表达式A⊕B × C时,先计算 B × C,其结果再与 A 做⊕运算。
现给定一个未完成的表达式,例如_+(_*_),请你在横线处填入数字00或者11 ,请问有多少种填法可以使得表达式的值为00。
输入输出格式
输入格式:
共 2 行。
第1 行为一个整数 LL,表示给定的表达式中除去横线外的运算符和括号的个数。
第2 行为一个字符串包含 LL 个字符,其中只包含’(’、’)’、’+’、’*’这44 种字符,其中’(’、’)’是左右括号,’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号。
输出格式:
共1 行。包含一个整数,即所有的方案数。注意:这个数可能会很大,请输出方案数对1000710007取模后的结果。
输入输出样例
说明
【输入输出样例说明】
给定的表达式包括横线字符之后为:_+(_*_)
在横线位置填入(0 、0 、0) 、(0 、1 、0) 、(0 、0 、1) 时,表达式的值均为0 ,所以共有3种填法。
【数据范围】
对于20\%20% 的数据有0 ≤ L ≤ 100≤L≤10。
对于50\%50% 的数据有 0 ≤ L ≤ 1,0000≤L≤1,000。
对于70\%70% 的数据有0 ≤ L ≤ 10,0000≤L≤10,000 。
对于100\%100%的数据有0 ≤ L ≤ 100,0000≤L≤100,000。
对于50\%50% 的数据输入表达式中不含括号。
就是一个十分有趣恶心的堆栈题
这里显然运用到了位运算(ex的东西)
运用堆栈,遇见*和(就入栈,遇见)就将(与)之间的符号出栈,遇见+就将前面的*出栈
以此来模拟(其中‘n’表示一个未知的数值)
直到最后算完表达式,输出为0的方案数
#include<bits/stdc++.h> using namespace std; inline void read(int &num) { bool flag=0; num=0; char c=getchar(); while((c<'0'||c>'9')&&c!='-') { c=getchar(); } if(c=='-') { flag=1; c=getchar(); } num=c-'0'; c=getchar(); while(c>='0'&&c<='9') { num=(num<<3)+(num<<1)+c-'0'; c = getchar(); } if(flag) { num*=-1; } } inline void output(int num) { if(num<0) { putchar('-'); num=-num; } if(num>=10) { output(num/10); } putchar(num%10+'0'); } inline void outln(int num) { output(num); } inline void outln(string str) { puts(str.c_str()); } const int mod=10007; const int N=100001; int n; char str[N];//输入的中缀表达式 stack<char> sta;//转后缀表达式时使用的栈 string final;//后缀表达式(答案序列) stack<int> zero, one;//zero维护使表达式值为0的方案个数,one维护使表达式值为1的方案个数 int main() { read(n); scanf("%s",str + 1); final.push_back('n');//后缀表达式最开始应该有一个未知变量 for(int i=1;i<=n;i++) { if(str[i]=='('||str[i]=='*')//遇到左括号或乘号,入栈 { sta.push(str[i]); } if(str[i]=='+')//遇到加号,弹出栈顶的乘号,然后加号入栈 { while(!sta.empty()&&sta.top()=='*') { final.push_back(sta.top()); sta.pop(); } sta.push(str[i]); } if(str[i]==')')//右括号,把到上一个左括号的元素出栈放入答案序列 { while(sta.top()!='(') { final.push_back(sta.top()); sta.pop(); } sta.pop(); } if(str[i]!='('&&str[i]!=')')//当不是左括号或者右括号时,应该插入一个未知变量 { final.push_back('n'); } } while(!sta.empty())//剩下的元素放入答案序列 { final.push_back(sta.top()); sta.pop(); } for(int i=0;i<final.size();i++) { char c=final[i]; { if(c=='n')//单个变量,方案数为1 { one.push(1); zero.push(1); } else { int rone=one.top(),rzero=zero.top();//rone表示右操作数(即上文中的y)为1的方案数(即上文中的y1),rzero同理 one.pop(),zero.pop(); int lone=one.top(),lzero=zero.top();//同理 one.pop(); zero.pop(); if(c == '*')//与操作,为1需要都为1,为0需要不都为1 { one.push(lone*rone%mod); zero.push((lone*rzero%mod+lzero*rone%mod+lzero*rzero%mod)%mod); } else//或操作,为0需要都为0,为1需要不都为0 { zero.push(lzero*rzero%mod); one.push((lone*rzero%mod+lzero*rone%mod+lone*rone%mod)%mod); } } } } outln(zero.top());//需要整个表达式的值为0 return 0; }