【USACO 2018 February Silver】Teleportation 题解

简化の题目：

求 (sumlimits_{i=1}^n{minleft{|a_i-b_i|,|a_i|+|y-b_i| ight}}) 的最小值

思路

对每一个 (y) ，考虑 (O(1)) 计算答案。

我们先计算出 (sum|a_i-b_i|) ，把求答案转换成求“节省”的最大值。

对于一组 (a_i,b_i) ，如果其经过传送门，那么传送门的终点一定在以 (b_i) 为中心点的一段区间上。同时，能节省的路程以 (b_i) 为中心向两边减少，也就是这样：

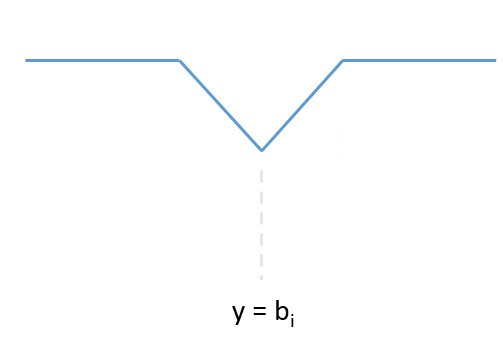
接下来，我们只要求出 (b_i) 处节省了多少，就能求出左端点和右端点。

有两种情况

1. (|a_i|ge|a_i-b_i|) 没有节省，不用管，去到传送门的距离大于等于两点距离。

2. (|a_i|<|a_i-b_i|) 节省了 (|a_i-b_i|-|a_i|) 即两点距离减去到传送门的距离。

如果是第二种情况，那么左端点就为：(b_i-|a_i-b_i|+|a_i|)

右端点为：(b_i+|a_i-b_i|-|a|)

就是中心点加减节省了多少

USACO的题解分成了两种情况，其实就是把绝对值拆开了。

害我研究半天，最后只能自己推

得到左中右端点之后，把左端点的斜率减1，中间点的斜率加2，右端点的斜率减1（想想为什么）。

统计答案时用差分的方法，把所有的“节省线段”叠加起来（加起来，具体证明请意会），得到当前点的“节省值”比上一个点增加（或减少）了多少，然后统计答案。

实现

在更改某个点的斜率时，使用平衡树（map），或离散化解决空间问题。同时，我们发现某个端点一定可以得到答案（感性理解：一个线段的最低点一定在端点上）。所以，我们可以只计算端点，用斜率乘距离来差分，即可统计答案。

代码

#include<map>
#include<cmath>
#include<cstdio>
#include<iostream>
using namespace std;
int n,a,b;
map<int,int>f;
long long ans;
void read(int &x){
	char c=getchar();
	for(;c<33;c=getchar());
	int f=1;
	if(c=='-'){
		f=-1;
		c=getchar();
	}
	for(x=0;(c>47)&&(c<58);x=x*10+c-48,c=getchar());
	x*=f;
}
int main(){
	freopen("teleport.in","r",stdin);
	freopen("teleport.out","w",stdout);
	read(n);
	for(int i=1;i<=n;i++){
		read(a);read(b);
		ans+=abs(a-b);
		if(abs(a)<=abs(a-b)){
			f[b]+=2;    //中心
			f[b-abs(a-b)+abs(a)]--;    //左
			f[b+abs(a-b)-abs(a)]--;    //右
		}
	}
	long long c=ans,s=0,l=-0x7fffffff;
	for(map<int,int>::iterator i=f.begin();i!=f.end();i++){
		int y=i->first,fx=i->second;
		c+=s*(y-l);    //长度乘斜率
		l=y;     //当前结点为下一个的上一个
		s+=fx;    //叠加线段
		ans=min(ans,c);    //统计答案
	}
	printf("%lld",ans);
	fclose(stdin);
	fclose(stdout);
}