转载:转载请注明出处:勿在浮沙筑高台http://blog.csdn.net/luoshixian099/article/details/51908175
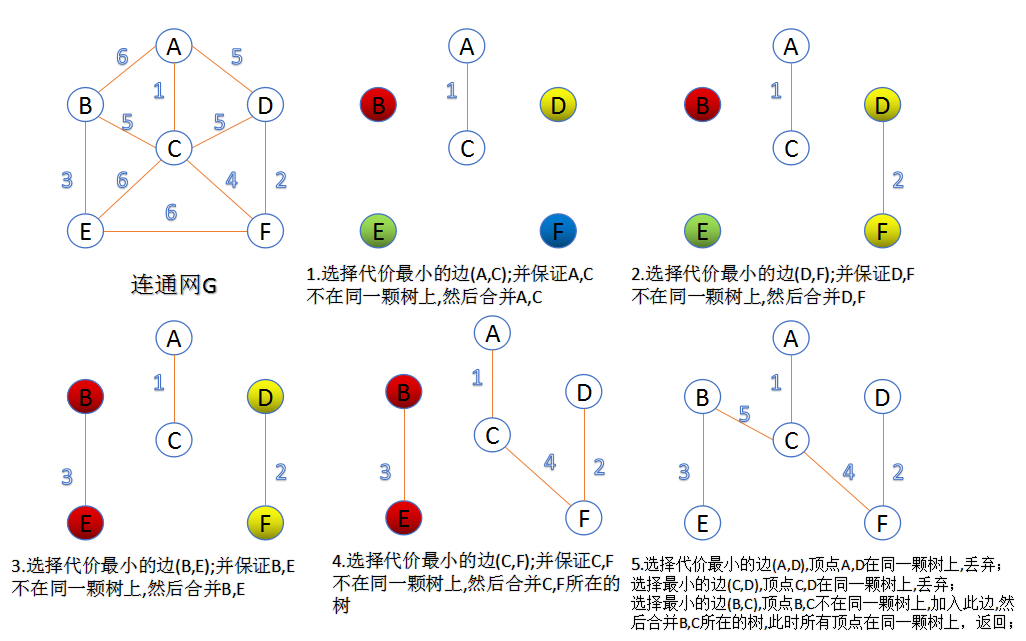
一.Prim算法
适用于:边较多时
加点法:
时间复杂度:O(V^2)
- 在已得最小生成树各个节点,(绿色set:A,C,G)
- 向外部其他节点的节点中(白色set:B,F,D),找到连边权值最小(2)的点(D),
- 加入最小生成树集合(->绿色set:A,C,G,D)。
直到:绿色set.size=sizeof(all node)
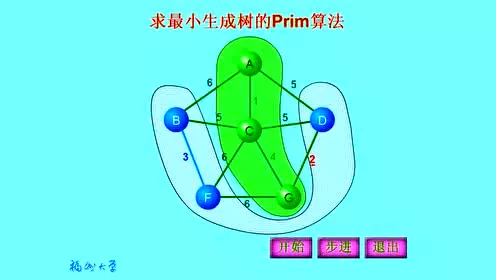
其他参考图:
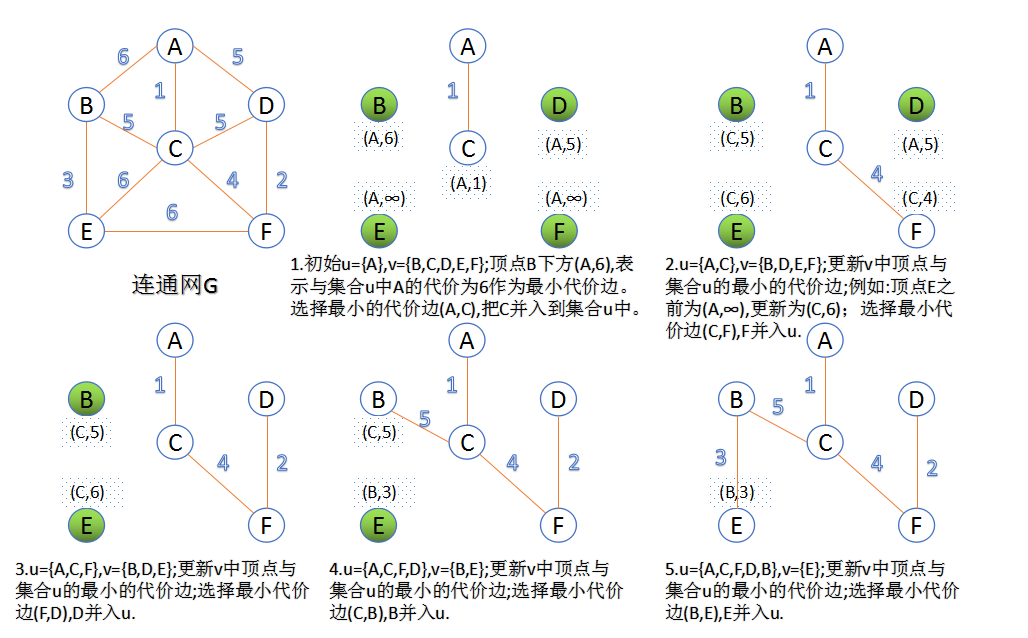
二.Kruskal 算法
适用于:边较少:稀疏图
加边法:
时间复杂度:O(ElogV)
- 将各个节点看作 各个独立的set(绿1:A,C,D; 绿2:B,F; 白:G)
- 选取能够连接的两个节点分属不同set的边(min{AB=6,FC=5,FG=6,GC=7,GD=6})。取权值最小者(FC:5最小)。
- 将该边连接的两个set合并为一个set(绿1+绿2 = A,D,C-F,B)。
直到:
- 绿色sizeof(one set edges) = n-1
- or sizeof(one set nodes) = sizeof(all node)
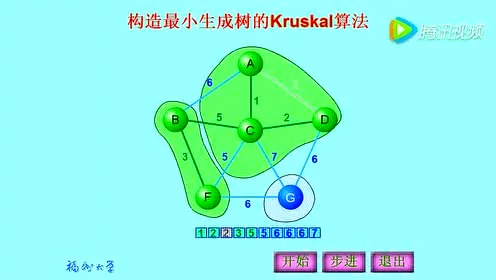
其他参考图: