1210. Minimum Moves to Reach Target with Rotations

问题：

给定由0和1构成的n*n二维数组，表示迷宫。

0代表通路，1代表障碍。

长度为2的蛇，

初始状态在第一行的前两个格子(0,0)<蛇尾>(0,1)<蛇头>

最终要到达最后一行的最后两个格子(n-1,n-2)<蛇尾>(n-1,n-1)<蛇头>

求最少走多少步能到。

移动选项：

• 向右移动一格：蛇头蛇尾 x不变，y+1
• 向下移动一格：蛇头蛇尾 x+1，y不变
• 旋转：
  • 条件：除了移动前后的cell都非障碍1外，还需corner cell也非 1。（如图：右下角cell）
  • 蛇的状态：水平->垂直：蛇尾不变，蛇头x+1，y-1
  • 
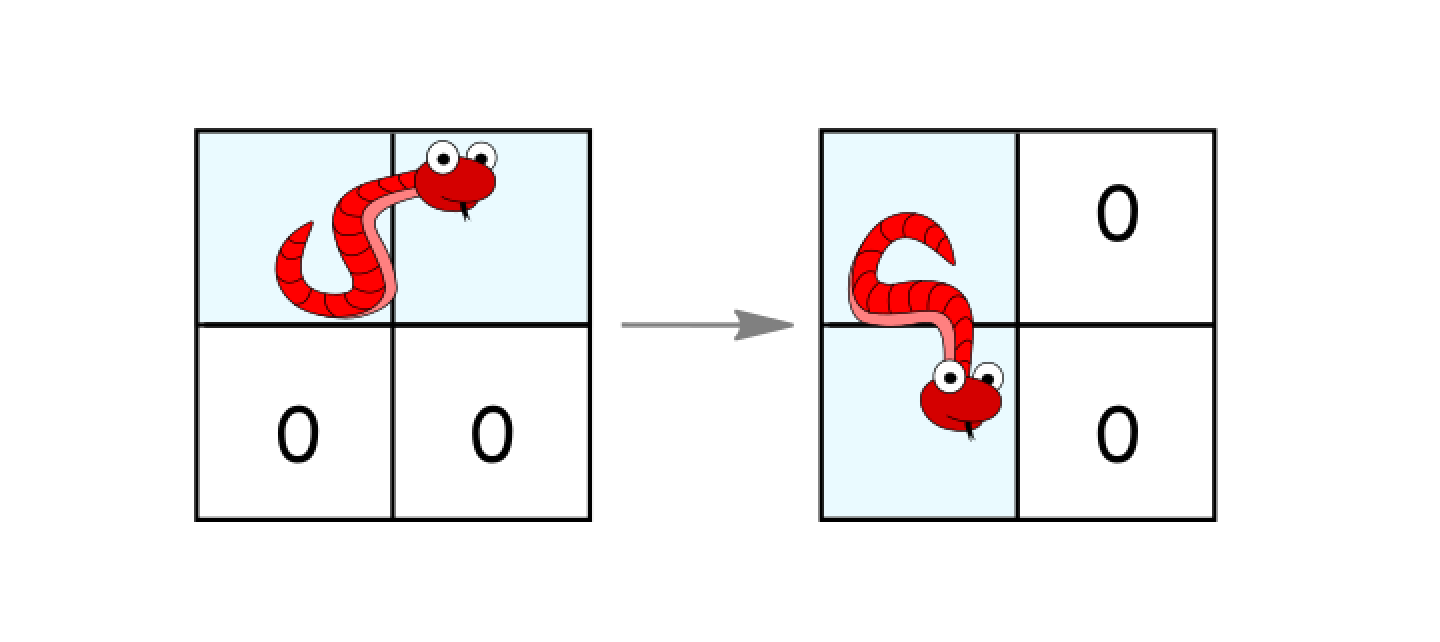
  • 蛇的状态：垂直->水平：蛇尾不变，蛇头x-1，y+1
  • 

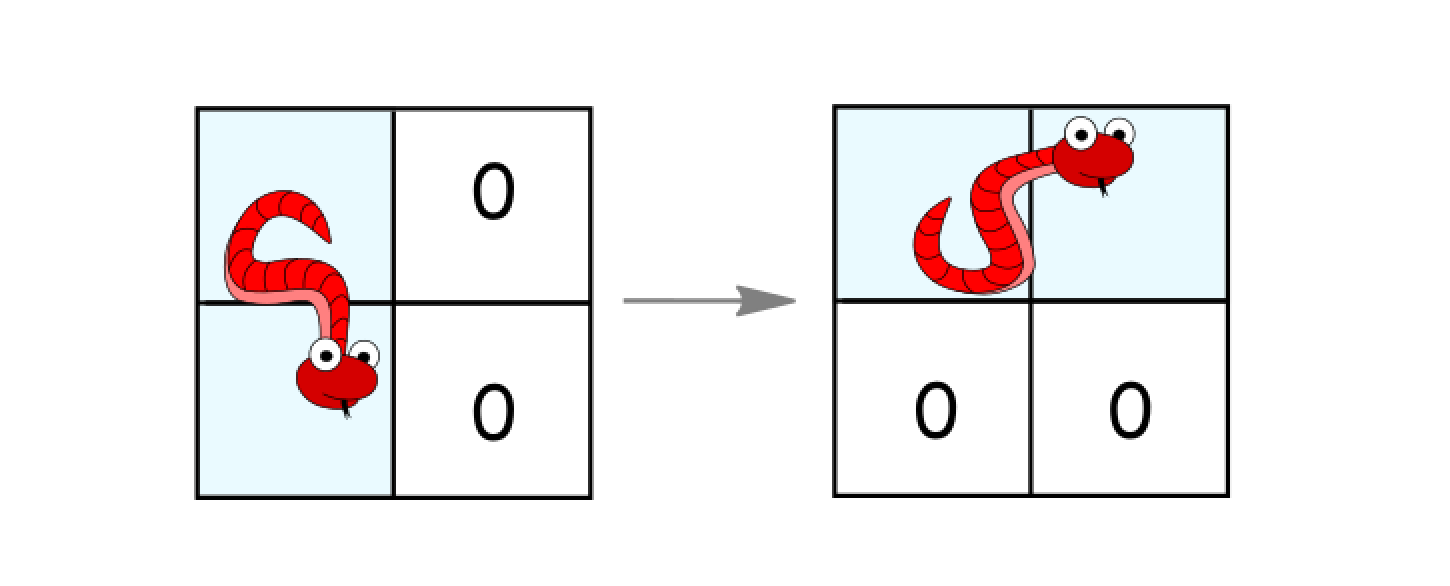
 解法：BFS

状态：蛇尾坐标(x,y)+蛇状态(H)（true:水平  or  false:垂直）；即可确定蛇头蛇尾。

• queue.push {x, y, H}
• visited->grid记录
  • bit 0: block or route
  • bit 1: 水平状态visited
  • bit 2: 垂直状态visited
• stp记录展开层数。

每次处理一个状态node：

若(x,y)=(n-1,n-2) && H==true ->target状态，返回stp

获得当前状态的水平垂直mask：maskHV=1<<(H?1:2);

判断下一个位置状态是否visited：

• 向右移动：gird[x][y+1] 的【H】状态：gird[x][y+1]&maskHV==1?
• 向下移动：gird[x+1][y] 的【H】状态：gird[x+1][y]&maskHV==1?
• 旋转：gird[x][y] 的【非H】状态：gird[x][y]&(maskHV=1<<(H?2:1))==1?

上述为非visited的情况下，看下一个移动是否合法：

• 向右移动：下一个状态的cell都在坐标范围内，且都 grid & 1==0:
  • 当前水平H：蛇尾(x,y) 蛇头(x,y+1)
    • 蛇尾：(x,y+1)
    • 蛇头：(x,y+1+1)
  • 当前垂直～H：蛇尾(x,y) 蛇头(x+1,y)
    • 蛇尾：(x,y+1)
    • 蛇头：(x+1,y+1)
• 向下移动：下一个状态的cell都在坐标范围内，且都 grid & 1==0:
  • 当前水平H：蛇尾(x,y) 蛇头(x,y+1)
    • 蛇尾：(x+1,y)
    • 蛇头：(x+1,y+1)
  • 当前垂直～H：蛇尾(x,y) 蛇头(x+1,y)
    • 蛇尾：(x+1,y)
    • 蛇头：(x+1+1,y)
• 旋转：下一个状态的cell都在坐标范围内，且都 grid & 1==0，且corner grid[x+1][y+1] &1==0:
  • 当前水平H：蛇尾(x,y) 蛇头(x,y+1)
    • 蛇尾：(x,y)（不动）
    • 蛇头：(x+1,y+1-1)
  • 当前垂直～H：蛇尾(x,y) 蛇头(x+1,y)
    • 蛇尾：(x,y)（不动）
    • 蛇头：(x+1-1,y+1)

⚠️ 注意：水平垂直状态的转换：H?false:true

代码参考：

class Solution {
public:
    int n;
    //remember [tail] to mark position
    //tail: x,y
    //head: if(horizontal--) x,y+1
    //      if(vertical || ) x+1,y
    //MOVE ->: tail: x, y+1; HV: not change
    //          precondition： H: (y+1),y+2<n; tail,head: grid[x][(y+1),y+2]==0
    //                        V: y+1<n; tail:grid[x][y+1]==0; head:grid[x+1][y+1]==0
    //MOVE ↓:  tail: x+1, y; HV: not change
    //          precondition： H: x+1<n; tail:grid[x+1][y]==0; head:grid[x+1][y+1]==0
    //                        V: (x+1),x+2<n; tail:grid[(x+1),x+2][y]==0;
    //ROTATE:  tail: x, y; HV: ~HV(T->F,F->T)
    //        precondition： H:x+1<n; head: grid[x+1][y]==0; corner: grid[x+1][y+1]==0
    //         ↓            V:y+1<n; head: grid[x][y+1]==0; corner: grid[x+1][y+1]==0
    //        H&V combination: x+1<n && y+1<n
    //                       && grid[x+1][y]==0 && grid[x][y+1]==0 && corner: grid[x+1][y+1]==0
    //queue cell: {tail[0],tail[1],hori?vert?}
    //visited:MARK grid-> bit_0 (1<<0): block or not
    //                    bit_1 (1<<1): H:visited
    //                    bit_2 (1<<2): V:visited
    bool canGoRight(vector<vector<int>>& grid, int x, int y, int H) {
        //cout<<"Goright"<<endl;
        if(H) return y+2<n && (grid[x][y+2]&1)==0;
        return y+1<n && (grid[x][y+1]&1)==0 && (grid[x+1][y+1]&1)==0;
    }
    bool canGoDown(vector<vector<int>>& grid, int x, int y, int H) {
        //cout<<"canGoDown"<<endl;
        if(H) return x+1<n && (grid[x+1][y]&1)==0 && (grid[x+1][y+1]&1)==0;
        return x+2<n && (grid[x+2][y]&1)==0;
    }
    bool canRotate(vector<vector<int>>& grid, int x, int y) {
        //cout<<"canRotate"<<endl;
        return x+1<n && y+1<n &&
            (grid[x+1][y]&1)==0 && (grid[x][y+1]&1)==0 && (grid[x+1][y+1]&1)==0;
    }
    int minimumMoves(vector<vector<int>>& grid) {
        n = grid.size();
        queue<array<int,3>> q;
        q.push({0,0,true});//source: --
        grid[0][0]|=(1<<1);
        int stp = 0;
        int maskHV;
        while(!q.empty()) {
            int sz = q.size();
            for(int i=0; i<sz; i++) {
                auto [x,y,H] = q.front();
                q.pop();
                if(x==n-1 && y==n-2 && H) return stp;//target: --
                maskHV = 1<<(H?1:2);
                //cout<<"pop:[x,y,H]:"<<x<<","<<y<<","<<H<<",maskHV:"<<maskHV<<endl;
                //cout<<((grid[x][y+1]&maskHV==0))<<endl;
                if(y+1<n && (grid[x][y+1]&maskHV)==0//->
                   && canGoRight(grid, x, y, H)) {
                    //cout<<"R push:[x,y,H]:"<<x<<","<<y+1<<","<<H<<endl;
                    q.push({x,y+1,H});
                    grid[x][y+1]|=maskHV;
                }
                if(x+1<n && (grid[x+1][y]&maskHV)==0//↓
                   && canGoDown(grid, x, y, H)) {
                    //cout<<"D push:[x,y,H]:"<<x+1<<","<<y<<","<<H<<endl;
                    q.push({x+1,y,H});
                    grid[x+1][y]|=maskHV;
                }
                maskHV = 1<<(H?2:1);
                if((grid[x][y]&maskHV)==0
                  && canRotate(grid,x,y)) {
                    //cout<<"RO push:[x,y,H]:"<<x<<","<<y<<","<<~H<<endl;
                    q.push({x,y,H?false:true});
                    grid[x][y]|=maskHV;
                }
            }
            stp++;
        }
        return -1;
    }
};