约瑟夫问题合集

swustoj 142

猴子报数(0142)
Time limit(ms): 1000Memory limit(kb): 65535Submission: 1338Accepted: 830

问题描述：n个猴子围坐一圈并按照顺时针方向从1到n编号，从第s个猴子开始进行1到m的报数，报数到第m的猴子退出报数，从紧挨它的下一个猴子重新开始1到m的报数，如此进行下去知道所有的猴子都退出为止。求给出这n个猴子的退出的顺序表。

输入：有做组测试数据．每一组数据有两行，第一行输入n（表示猴子的总数最多为100）第二行输入数据s(从第s个猴子开始报数)和数据m(第m个猴子退出报数)．当输入０　０　０时表示程序结束．

输出：每组数据的输出结果为一行，中间用逗号间隔。

样例输入：

10
2 5
5
2 3
0
0 0

样例输出：

6,1,7,3,10,9,2,5,8,4
4,2,1,3,5

#include <stdio.h>
int main()
{
    int i,j;
    int p[110];
    int n,m,k,ret;
    while(scanf("%d%d%d",&n,&m,&k),n||m||k)
    {
        ret=m;
        for(int i=1;i<=n;i++) p[i]=i;
        while(n)
        {
            ret=(ret+k-2)%n+1;
            if(n>1) printf("%d,",p[ret]);
            else printf("%d
",p[ret]);
            for(j=ret;j<n;j++)
            {
                p[j]=p[j+1];
            }
            n--;
        }
    }
    return 0;
}

HDU 2925

Musical ChairsTime 

Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 1176    Accepted Submission(s): 680

Problem Description In the traditional game of Musical Chairs, N + 1 children run around N chairs (placed in a circle) as long as music is playing. The moment the music stops, children run and try to sit on an available chair. The child still standing leaves the game, a chair is removed, and the game continues with N children. The last child to sit is the winner.

In an attempt to create a similar game on these days' game consoles, you modify the game in the following manner: N Children are seated on N chairs arranged around a circle. The chairs are numbered from 1 to N . Your program pre-selects a positive number D . The program starts going in circles counting the children starting with the first chair. Once the count reaches D , that child leaves the game, removing his/her chair. The program starts counting again, beginning with the next chair in the circle. The last child remaining in the circle is the winner.
For example, consider the game illustrated in the figure above for N = 5 and D = 3 . In the figure, the dot indicates where counting starts and × indicates the child leaving. Starting off, child #3 leaves the game, and counting restarts with child #4. Child #1 is the second child to leave and counting restart with child #2 resulting in child #5 leaving. Child #2 is the last to leave, and child #4 is the winner. Write a program to determine the winning child given both N and D .  
Input Your program will be tested on one or more test cases. Each test case specifies two positive integers N and D on a single line, separated by one or more spaces, where N, D < 1, 000, 000 .
The last line of the input file contains two 0's and is not part of the test cases.  
Output For each test case, write the winner using the following format:
N D W
Where N and D are as above, is a space character, and W is the winner of that game.  
Sample Input 5 37 40 0  
Sample Output 5 3 47 4 2  

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define N 1010

int n,k;

int main()
{
    int i,res;
    while(scanf("%d%d",&n,&k),n||k)
    {
        res=0;
        for(i=2;i<=n;i++)
        {
            res=(res+k)%i;
        }
        printf("%d %d %d
",n,k,res+1);
    }
    return 0;
}

POJ 3517

And Then There Was One

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 4865		Accepted: 2592

Description

Let’s play a stone removing game.

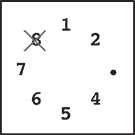
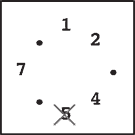
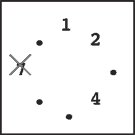
Initially, n stones are arranged on a circle and numbered 1, …, n clockwise (Figure 1). You are also given two numbers k and m. From this state, remove stones one by one following the rules explained below, until only one remains. In step 1, remove stone m. In step 2, locate the k-th next stone clockwise from m and remove it. In subsequent steps, start from the slot of the stone removed in the last step, make k hops clockwise on the remaining stones and remove the one you reach. In other words, skip (k − 1) remaining stones clockwise and remove the next one. Repeat this until only one stone is left and answer its number. For example, the answer for the case n = 8, k = 5, m = 3 is 1, as shown in Figure 1.

Initial state	Step 1	Step 2	Step 3	Step 4
Step 5	Step 6	Step 7	Final state

Figure 1: An example game

Initial state: Eight stones are arranged on a circle.

Step 1: Stone 3 is removed since m = 3.

Step 2: You start from the slot that was occupied by stone 3. You skip four stones 4, 5, 6 and 7 (since k = 5), and remove the next one, which is 8.

Step 3: You skip stones 1, 2, 4 and 5, and thus remove 6. Note that you only count stones that are still on the circle and ignore those already removed. Stone 3 is ignored in this case.

Steps 4–7: You continue until only one stone is left. Notice that in later steps when only a few stones remain, the same stone may be skipped multiple times. For example, stones 1 and 4 are skipped twice in step 7.

Final State: Finally, only one stone, 1, is on the circle. This is the final state, so the answer is 1.

Input

The input consists of multiple datasets each of which is formatted as follows.

n k m

The last dataset is followed by a line containing three zeros. Numbers in a line are separated by a single space. A dataset satisfies the following conditions.

2 ≤ n ≤ 10000, 1 ≤ k ≤ 10000, 1 ≤ m ≤ n

The number of datasets is less than 100.

Output

For each dataset, output a line containing the stone number left in the final state. No extra characters such as spaces should appear in the output.

Sample Input

8 5 3
100 9999 98
10000 10000 10000
0 0 0

Sample Output

1
93
2019

Source

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define N 1010

int n,m,k;

int main()
{
    int i,res;
    while(scanf("%d%d%d",&n,&k,&m),n||m||k)
    {
        res=0;
        for(i=2;i<=n-1;i++)
        {
            res=(res+k)%i;
        }
        printf("%d
",(res+m)%n+1);
    }
    return 0;
}

HIT 1016

Joseph's problem I

The Joseph's problem is notoriously known. For those who are not familiar with the problem, among n people numbered 1,2...n, standing in circle every m_th is going to be executed and only the life of the last remaining person will be saved. Joseph was smart enough to choose the position of the last remaining person, thus saving his life to give the message about the incident.

Although many good programmers have been saved since Joseph spread out this information, Joseph's cousin introduced a new variant of the malignant game. This insane character is known for its barbarian ideas and wishes to clean up the world from silly programmers. We had to infiltrate some the agents of the ACM in order to know the process in this new mortal game.

In order to save yourself from this evil practice, you must develop a tool capable of predicting which person will be saved.

The Destructive Process

The persons are eliminated in a very peculiar order; m is a dynamical variable, which each time takes a different value corresponding to the prime numbers' succession (2,3,5,7...). So in order to kill the ith person, Joseph's cousin counts up to the i_th prime.

Input

It consists of separate lines containing n [1..3501], and finishes with a 0.

Output

The output will consist in separate lines containing the position of the person which life will be saved.

Sample Input

6

Sample Output

4

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define N 100000

int tot;
bool isprime[N+10];
int prime[N+10];

void init()
{
    tot=0;
    memset(isprime,1,sizeof(isprime));
    isprime[0]=isprime[1]=0;
    for(int i=2;i<=N;i++)
    {
        if(isprime[i]) prime[tot++]=i;
        for(int j=0;j<tot;j++)
        {
            if(i*prime[j]>N) break;
            isprime[i*prime[j]]=0;
            if(i%prime[j]==0) break;
        }
    }
}
int main()
{
    init();
    int n,ret;
    while(scanf("%d",&n),n)
    {
        ret=0;
        for(int i=2;i<=n;i++)
        {
            ret=(ret+prime[n-i])%i;
        }
        printf("%d
",ret+1);
    }
    return 0;
}