零、转置卷积介绍
一、棋盘效应

当我们要用到深度学习来生成图像的时候,是往往是基于一个低分辨率且具有高层语义的图像。这会使得深度学习来对这种低分辨率图像进行填充细节。一般来说,为了执行从低分辨率图像到高分辨率图像之间的转换,我们往往要进行deconvolution。简单来说,deconvolution layer可以允许模型通过每一个点进行绘制高分辨率图像上的一个方块,这种情况的产生与deconvolution的stride、kernel size有关。
问题产生:kernel size无法被stride整除
stride为1,kernel size为3,这导致了重复上采样绘图的部分不均匀(下图深色部分),
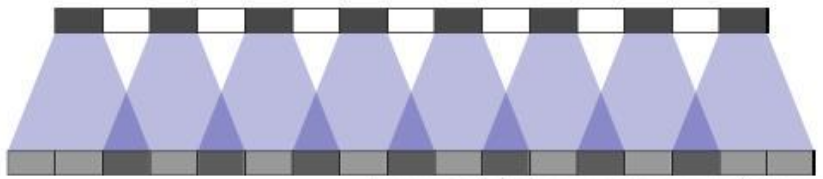
二维情况更为严重,
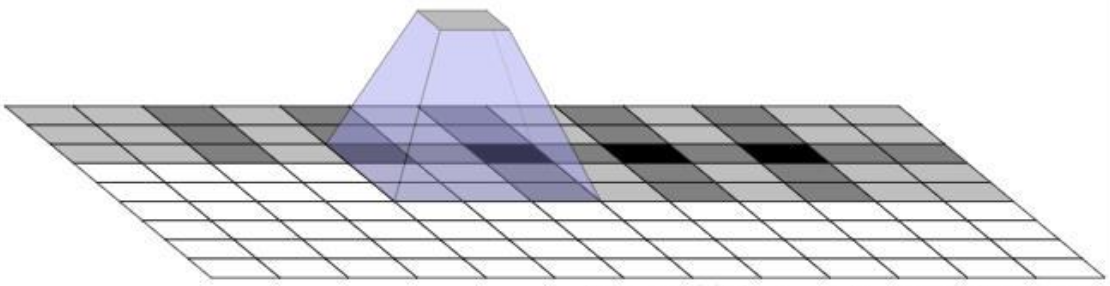
思路一:多层重复转置卷积
一个常见的想法是寄希望于多层重复转置卷积,希望能抵消掉棋盘效应,但是实际上一般事与愿违,
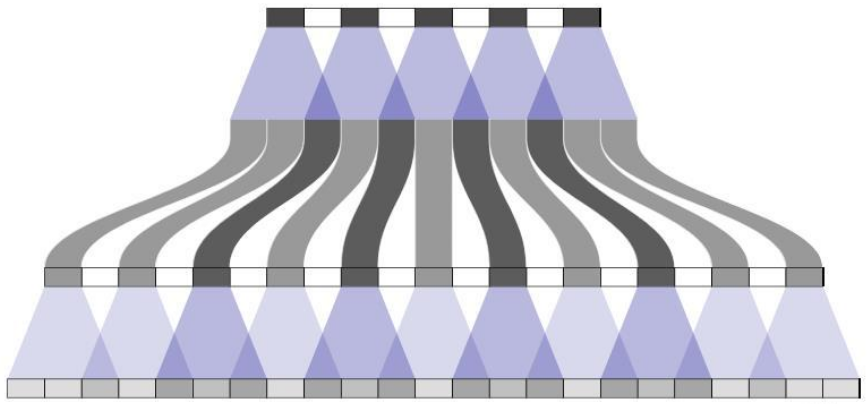
重复的结构使得棋盘更加复杂。
思路二:stride为1的转置卷积
此时可以很好地解决这个问题,

但是……转置卷积的意义在于上采样,stride为1还上采毛线……,所以一般会用于卷积栈的末尾作为调整,不过效果有限,

思路三:调整kernel权重分布
加大无重叠部分的权重分布可以很好的解决的这个问题,原理如下图:

但是这种做法会极大地限制模型的学习能力(避免棋盘效应往往会降低模型容量,会使得模型变得更大从而使得难以训练。原文的话是指: Avoiding artifacts significantly restricts the possible filters, sacrificing model capacity)
二、更好的上采样
方法一:采取可以被stride整除的kernel size
该方案较好的应对了棋盘效应问题,但是仍不够圆满,因为一旦我们的kernel学习不均匀,仍然会产生棋盘效应,

在上图中,我们的weight并不够平衡,这直接导致了输出的棋盘效应。
即便如此,采用这个思路去设计网络仍然是必要的。
方法二:插值
可以直接进行插值resize操作,然后再进行卷积操作。这种操作在超分辨率文献中很常见。例如,我们可以采取近邻插值或者样条插值来进行上采样。
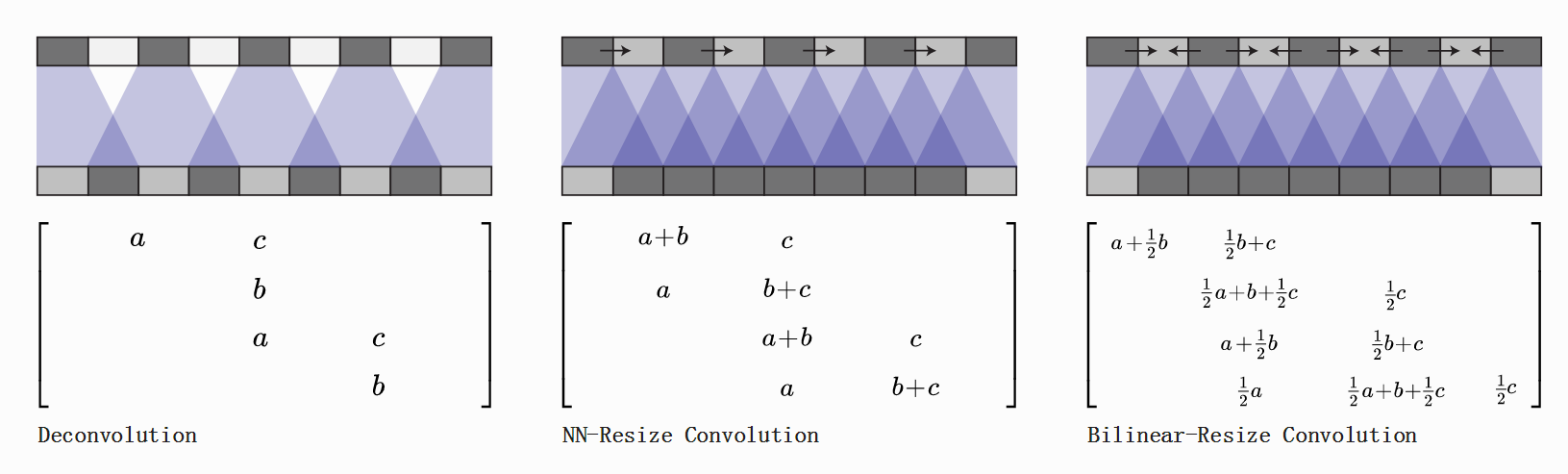
有关上图的三个矩阵不是很理解,不过方法给了,就是先插值再卷积,这在我之前的项目DCGAN_TensorFlow有应用, 可以参考。