You are given n numbers a1, a2, ..., an. You can perform at most k operations. For each operation you can multiply one of the numbers by x. We want to make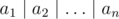 
as large as possible, where 
denotes the bitwise OR.
Find the maximum possible value of 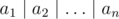after performing at most k operations optimally.
The first line contains three integers n, k and x (1 ≤ n ≤ 200 000, 1 ≤ k ≤ 10, 2 ≤ x ≤ 8).
The second line contains n integers a1, a2, ..., an (0 ≤ ai ≤ 109).
Output the maximum value of a bitwise OR of sequence elements after performing operations.
3 1 2
1 1 1
3
4 2 3
1 2 4 8
79
For the first sample, any possible choice of doing one operation will result the same three numbers 1, 1, 2 so the result is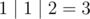 
.
For the second sample if we multiply 8 by 3 two times we'll get 72. In this case the numbers will become 1, 2, 4, 72 so the OR value will be 79 and is the largest possible result
题意：给你一个长度为n的序列 可以执行k次操作 每次操作可以将序列中的任意一个数乘以x
使得最后的连续OR（|运算）的值最大
题解：为了使得最后的值很大 应该将增益集中在某一位上 使得高位不断左移
但是应该增加在哪一位上呢？并不是一定增加在现有序列的最大值上 有hack数据
3 1 2
4 5 6
所以直接暴力枚举 寻找最大值 但是需要先预处理前缀或 后缀或 具体看代码
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #define ll __int64 6 using namespace std; 7 ll n,k,x; 8 ll a[200005]; 9 ll exm; 10 ll gg; 11 ll ans1[200005]; 12 ll ans2[200005]; 13 ll ma; 14 int main() 15 { 16 ma=0; 17 scanf("%I64d %I64d %I64d ",&n,&k,&x); 18 for(ll i=1;i<=n;i++) 19 scanf("%I64d",&a[i]); 20 exm=1; 21 for(ll i=1;i<=k;i++) 22 exm*=x; 23 ll s=0; 24 ans1[0]=0; 25 for(ll i=1;i<=n;i++)//前缀 26 { 27 s=(s|a[i]); 28 ans1[i]=s; 29 } 30 s=0; 31 ans2[n+1]=0; 32 for(ll i=n;i>=1;i--)//后缀 33 { 34 s=(s|a[i]); 35 ans2[i]=s; 36 } 37 for(ll i=1;i<=n;i++) 38 ma=max(ma,ans1[i-1]|(a[i]*exm)|ans2[i+1]); 39 cout<<ma<<endl; 40 return 0; 41 }